Lihong Li, Wei Chu, John Langford, Robert E. Schapire의 A Contextual-Bandit Approach to Personalized News Article Recommendation을 번역했습니다.

초록

개인화 웹 서비스는 콘텐츠 및 사용자 정보를 이용해서 개별 사용자에게 (광고, 뉴스 기사 등의) 맞춤 서비스를 제공하기 위해 노력한다. 최신 기술의 발전에도 불구하고 적어도 두 가지 이유로 여전히 난항을 겪고 있다. 먼저, 웹 서비스의 경우 기존 협업 필터링 방법을 적용하기 어려울 만큼 동적으로 변하는 콘텐츠 풀을 특징으로 한다. 둘째, 실용적으로 자주 쓰이는 웹 서비스의 규모는 학습과 계산 모든 면에서 고속인 해법을 필요로 한다.

본 논문은 뉴스 기사 개인화 추천을 어떤 원리적 접근법, 컨텍스츄얼 밴딧 문제로 모형화한다. 컨텍스츄얼 밴딧은 사용자 클릭 수 총합을 최대로 만들기 위해 사용자 클릭 피드백을 바탕으로 기사 선택 전략을 점차 수정해 나가는 동시에 사용자와 기사에 관한 맥락 상 정보를 바탕으로 사용자에게 제공할 기사를 순차적으로 선택하는 학습 알고리즘이다.

이 논문이 공헌하는 바는 세 가지이다. 첫째, 계산이 효율적이며 학습 이론에서 동기를 얻은, 새롭고 일반화 가능한 컨텍스츄얼 밴딧 알고리즘을 제안한다. 둘째, 이전에 기록된 무작위 트래픽을 이용하여 모든 밴딧 알고리즘을 오프라인에서 안정적으로 평가할 수 있는 방법을 이야기한다. 마지막으로 해당 오프라인 평가 방법을 통해 3,300만 건이 넘는 이벤트가 포함된 Yahoo! Front Page Today 데이터셋에 새 알고리즘을 성공적으로 적용했다. 결과에 따르면 기존의 맥락 무관한 밴딧 알고리즘과 비교했을 때 클릭 수준을 12.5% 넘게 끌어올렸고 이러한 장점은 데이터가 부족할수록 더욱 커진다.

1. 서론

본 논문은 각 사용자 별로 가장 적절한 웹 기반 콘텐츠를 가장 적절한 시기에 선별하는 문제를 해결한다. 대부분의 서비스 공급 업체는 예를 들어 뉴스 기사를 필터링하거나 광고를 띄우기 위해 저장소에 다량의 콘텐츠를 확보하고 유지 관리한다. 또한 그러한 웹 서비스 저장소의 콘텐츠는 빈번한 추가 및 삭제를 거치면서 동적으로 변한다. 이러한 환경에서 사용자가 흥미를 가질 콘텐츠를 신속히 선정해내는 게 중요하다. 예를 들자면 뉴스 필터는 인기 있는 속보를 즉시 판별해내는 동시에 시간이 흐른, 기존 뉴스 기사의 가치는 감가시켜야한다.

콘텐츠 정보 만으로 인기와 시간에 따른 변화를 모형화하는 건 일반적으로 어렵다. 보통 실무에서는 신규 콘텐츠의 인기를 평가하기 위해 소비자 피드백을 실시간으로 수집해 미지의 것을 탐색해봄과 함께 기존 가치의 변화를 추적, 관측해나간다. 예를 들어 트래픽 일부를 그러한 탐색을 위해 배정할 수 있다. 무작위로 고른 콘텐츠에 대한 트래픽 일부의 사용자 응답(예: 클릭)을 기반으로 가장 애용되는 콘텐츠를 판별해서 이를 나머지 트래픽에 활용해볼 수 있다. 트래픽 중 \(\epsilon\)만큼의 부분은 무작위로 탐색하고 나머지에 대해 탐욕적 활용을 수행하는 해당 전략을 \(\epsilon\)-탐욕이라고 부른다. EXP3이나 UCB1과 같이 진보한 탐색 접근법도 사용해볼 수 있다. 직관적으로 신규 콘텐츠의 경우 더 많은 트래픽을 배정해서 가치를 빨리 학습해야 하고 기존 콘텐츠의 경우 추이를 파악하기 위한 사용자 수는 점차 줄여 나가야 한다.

최근 개인화 추천은 웹 사이트가 개별 사용자 요구에 맞게 콘텐츠 표현을 조정하여 사용자 만족도를 향상하는 용도로써 훌륭히 잘 쓰이고 있다. 개인화는 사용자 속성을 수집, 저장하고 콘텐츠 자산을 관리하며 현재와 과거 사용자 행동을 분석하여 가장 적합한 콘텐츠를 현 사용자에게 개별적으로 제공하는 절차를 포함한다.

사용자와 콘텐츠는 흔히 변수의 집합으로 표현된다. 사용자 변수에는 기입된 인구 통계 정보뿐만 아니라 활동 기록을 집계한 걸 포함시킬 수 있다. 콘텐츠 변수에는 설명 정보와 범주를 포함시킬 수 있다. 지금 다루는 시나리오의 경우 똑같은 콘텐츠에 대해 사용자마다 관점이 상당히 다를 수 있기 때문에 탐색과 활용이 개별적으로 수행되어야 한다. 매우 많은 숫자의 선택지 또는 동작이 존재할 수 있으므로 콘텐츠 품목 간의 공통점을 인지하여 콘텐츠 풀로 해당 지식을 전달할 수 있는지도 중요하다.

협업 필터링, 콘텐츠 기반 필터링 또는 혼합 접근법을 포함하여 기존 추천 시스템은 과거 활동을 통해 판별한 사용자 관심사를 이용하여 개인 수준에서 의미 있는 추천을 제공한다. 사용자 간 소비 이력이 상당히 겹치고 콘텐츠 전체 목록이 잘 변하지 않는 시나리오라면 협업 필터링이 사용자 소비 이력을 기반으로 유사도를 계산하여 좋은 추천 안을 제공할 수 있다. 콘텐츠 기반 필터링의 경우 기존 사용자의 소비 프로필과 잘 부합하는 신규 품목을 식별하는데 용이하지만 추천한 품목이 사용자가 이전에 취해온 품목들과 굉장히 유사할 수밖에 없다. 혼합 접근법은 추천 기법을 두 가지 이상 결합하여 개발한다. 예를 들어 협업 필터링은 신규 품목을 추천할 수 없는데 보통 콘텐츠 기반 필터링과 결합하여 이 약점을 보완한다.

그러나 위에서 언급했듯이 대부분의 웹 기반 시나리오에서 콘텐츠 전체 목록은 자주 변경되며 시간이 경과함에 따라 콘텐츠의 인기는 변한다. 또한 방문자의 상당수는 과거 소비 기록이 전혀 없는 신규 사용자들인데 이는 보통 콜드 스타트 상황으로 불린다. 앞서 언급한 문제들은 과거 사례 연구에서 볼 수 있듯이 추천 시스템의 전통적인 접근법을 적용하기 어렵게 만든다. 따라서 사용자와 콘텐츠 중 한쪽 또는 양쪽 모두 새로 등장한 것이라면 서로 잘 부합하는지 학습하는 과정이 필수이다. 그러나 해당 정보를 수집하는 건 비용이 많이 들고 사용자 만족도를 단기적으로 저하시킬 수 있다. 그러므로 장기적인 사용자 만족도를 최대화하고 사용자의 관심사와 콘텐츠가 잘 부합하는지 정보를 수집하는, 상충하는 두 가지 목표 간에 최적 균형점을 찾는 문제로 이어진다.

윗 문제는 사실 변수 기반의 탐색 / 활용 문제로 알려져 있다. 본 논문은 이를 어떤 원리적 접근법, 컨텍스츄얼 밴딧 문제로 수식화한다. 컨텍스츄얼 밴딧은 사용자 클릭 수 총합을 장기적으로 최대로 만들기 위해 사용자 클릭 피드백을 바탕으로 기사 선택 전략을 점차 수정해 나가는 동시에 사용자와 기사에 관한 맥락 상 정보를 기반으로 사용자에게 제공할 기사를 순차적으로 선택하는 학습 알고리즘이다. 2장에서는 다중 슬롯머신 실험 문제를 정의하고 기존의 접근법을 검토한다. 그리고 3장에서 새로운 알고리즘 LinUCB를 제안한다. 해당 알고리즘의 경우 적은 계산양으로 최적 선형 예측자에 견주기 위해 가장 잘 알려진 알고리즘 기준으로 유사 리그릿 분석을 수행한다. 또 4장은 오프라인 평가 방법론을 다루면서 각 상호 작용이 독립이고 분포가 동일하다면(i.i.d.) 모든 탐색 / 활용 전략에 해당 전략을 적용할 수 있음을 증명한다. 서로 다른 사용자를 고려할 때 이는 합리적인 가정일 수 있다. 마지막으로 5장은 해당 오프라인 평가 전략을 사용하여 새 알고리즘과 기존 알고리즘을 실험한다.

2. 수식화와 연관 작업

이 장은 \(K\)개의 슬롯 손잡이를 갖는 컨텍스츄얼 밴딧 문제를 수식으로 정의하고 이것을 뉴스 기사 개인화 추천 문제에 어떻게 적용할 수 있는지 보인다. 그런 다음 기존 방법과 그 한계점을 논한다.

2.1 다중 슬롯머신 실험 문제 수식화

뉴스 기사 개인화 추천 문제는 자연스럽게 맥락 상의 정보가 있는 다중 슬롯머신 문제로 모형화할 수 있다. 이전 연구에 따라 이를 컨텍스츄얼 밴딧¹이라고 부를 것이다. 수식화해보자면 컨텍스츄얼 밴딧 알고리즘 \(\mathsf{A}\)는 개별 시도 \(t = 1, 2, 3, \ldots \)에 따라 수행된다. \(t\)번째 시도에 대하여,

1.알고리즘은 현재 사용자 \(u_t\)와 슬롯 손잡이 또는 행동의 집합 \(\mathcal{A}_t\)와 함께 \(a_t \in \mathcal{A}\)일 때의 변수 벡터 \(\mathbf{x}_{t, a}\)를 관측한다. 벡터 \(\mathbf{x}_{t, a}\)는 사용자 \(u_t\)와 슬롯 손잡이 \(a\)의 정보를 모두 축약하며 이를 맥락이라고 지칭한다.

2.이전 시도에서 관측한 손익에 기초하여 \(\mathsf{A}\)는 슬롯 손잡이 \(a_t \in \mathcal{A}\)를 선택하고 손익 \(r_{t, a_t}\)를 받는다. 해당 손익의 기댓값은 사용자 \(u_t\)와 슬롯 손잡이 \(a_t\) 양쪽에 의존한다.

3.알고리즘은 새로운 관측치 \((\mathbf{x}_{t, a}, a_t, r_{t, a_t})\)를 이용하여 슬롯 손잡이 선택 전략을 개선한다. 여기에서 중요한 것은 선택하지 않은 슬롯 손잡이 \(a \ne a_t\)에 대해서는 관측한 피드백(즉, 손익 \(r_{t, a}\)) 또한 없다는 점이다. 이 사실로부터 이어지는 결론은 다음 절에서 좀 더 자세히 논의할 것이다.

상술한 과정에서 \(\mathsf{A}\)의 총 \(T\)번의 시도에 따른 손익을 \(\sum_{t = 1}^T r_{t, a}\)로 정의한다. 이와 비슷하게 총 \(T\)번의 시도에 따른 최적 손익의 기댓값을 \(\mathbf{E}[\sum_{t = 1}^T r_{t, a_t^*}]\)으로 정의한다. 여기서 \(a_t^*\)는 \(t\)번째 시도에서 손익의 기댓값이 최대인 슬롯 손잡이이다. 목표는 \(\mathsf{A}\)를 잘 설계하여 위의 총 손익 기댓값을 최대로 만드는 것이다. 이와 동치로써, 최적의 슬롯 손잡이 선택 전략 대비 리그릿을 최소로 만드는 알고리즘을 찾는 것이다. 여기서 알고리즘 \(\mathsf{A}\)의 총 \(T\)번 시도에 따른 리그릿 \(R_{\mathsf{A}}(T)\)는 다음과 같은 수식으로 정의된다.

일반적인 컨텍스츄얼 밴딧 문제에서 특별히 중요한 경우는 (ⅰ) 슬롯 손잡이 집합 \(\mathcal{A}_t\)가 변하지 않으며 모든 \(t\)마다 슬롯 손잡이가 \(K\)개이고 (ⅱ) 사용자 \(u_t\)(또는 이와 동치로 맥락 \((\mathbf{x}_{t, 1}, \cdots ,\mathbf{x}_{t, K})\))가 모든 \(t\)마다 동일한 문제이다. 즉 잘 알려진, \(K\)개의 슬롯 손잡이를 갖는 다중 슬롯머신 실험이다. 다중 슬롯머신 실험 알고리즘에게 슬롯 손잡이 집합과 맥락은 모든 시도에서 동일하다. 해당 유형을 맥락 무관한 다중 슬롯머신 실험이라고 부른다.

기사 추천의 관점에서 콘텐츠 풀에 속하는 기사를 하나의 슬롯 손잡이로 볼 수 있다. 제공한 기사를 클릭하면 손익은 1이고 그렇지 않으면 0이라고 하자. 이 손익 정의에 따라 어떤 기사의 손익 기댓값은 정확히 클릭률(CTR)이며 CTR이 최대인 기사를 선택하는 것과 사용자의 클릭 수 기댓값을 최대로 만드는 건 동일한 얘기다. 또한 다중 슬롯머신 실험 수식에서 손익의 기댓값을 최대로 만드는 것과 같다.

게다가 웹 서비스는 사용자 관심사를 유추하고 가장 관심을 보일 만한 뉴스 기사를 선택하는데 이용 가능한 사용자 정보를 보통 갖고 있다. 예를 들자면 10대 남성은 은퇴 계획보다는 iPod 제품 기사에 관심을 가질 가능성이 훨씬 크다. 따라서 사용자와 기사의 경우 그것을 간략히 표현해내는 유용한 정보의 변수 집합으로 “축약”할 수 있다. 이렇게 하면 다중 슬롯머신 실험 알고리즘은 특정 기사 / 사용자의 CTR 정보를 일반화할 수 있고 특히 신규 사용자와 기사에 대해 적합한 기사를 더 빨리 선택할 수 있다.

2.2 기존의 다중 슬롯머신 실험 알고리즘

다중 슬롯머신 실험의 경우 핵심 과제는 탐색과 활용 간의 균형점을 찾는 일이다. 수식 (1)의 리그릿을 최소로 만들고자 알고리즘 \(\mathsf{A}\)는 최적으로 보이는 슬롯 손잡이 선택에 과거의 경험을 활용한다. 허나 \(\mathsf{A}\)가 갖고 있는 지식이 부정확해서 최적으로 보이는 슬롯 손잡이가 실은 최선책이 아닐 수 있다. 이 원치 않는 상황을 피하고자 \(\mathsf{A}\)는 차선으로 보이는 슬롯 손잡이들을 실제로 선택해가며 정보를 더 많이 수집하는 식으로 탐색을 한다(예를 들자면 이전 절에서 정의한 다중 슬롯머신 실험 3 단계). 최적이 아닌 슬롯 손잡이가 선택될 수 있기에 탐색은 단기 리그릿을 증가시킨다. 그러나 슬롯 손잡이의 평균 손익에 관한 정보를 얻어서(즉, 탐색으로) 슬롯 손잡이들에 대한 \(\mathsf{A}\)의 추정치를 갱신해 나갈 수 있으므로 장기 리그릿을 결과적으로 감소시킨다. 온전히 탐색만 하거나 활용만 하는 알고리즘은 일반적으로 잘 작동하지 않으며 적당한 절충안이 필요하다.

맥락 무관한, \(K\)개의 슬롯 손잡이를 갖는 다중 슬롯머신 실험 문제는 통계학자들이 오랫동안 연구해왔다. 가장 단순하고 직관적인 알고리즘 중의 하나는 \(\epsilon\)-탐욕이다. 먼저 각 시도 \(t\)마다 해당 알고리즘은 모든 슬롯 손잡이 \(a\)의 평균 손익 \(\hat{\mu_{t, a}}\)를 추정해 나간다. 그런 다음 \(1 - \epsilon\)의 확률로 탐욕적 슬롯 손잡이(즉, 가장 높은 손익 추정치를 갖는 슬롯 손잡이)를 선택하며 \(\epsilon\) 확률로 슬롯 손잡이를 무작위 선택한다. 극한을 취한다면 모든 슬롯 손잡이를 무한히 자주 시도할 것이다. 그래서 손익 추정치 \(\hat{\mu_{t, a}}\)는 1의 확률로 참값 \(\mu_a\)에 수렴한다. 더욱이 탐색 확률을 적절히 감소시키면 매 단계 당 리그릿, 즉 \(R_{\mathsf{A}}(T) / T\)는 1의 확률로 0에 수렴한다.

\(\epsilon\)-탐욕이 사용하는, 유도하지 않는 성향의 탐색 전략과 다르게 보통 신뢰 상한 알고리즘이라고 불리는 또 다른 범주의 알고리즘은 탐색과 활용 간 균형점을 찾기 위해 더 영리한 방법을 사용한다. 구체적으로 이 알고리즘은 각 슬롯 손잡이 \(a\)의 평균 손익 \(\hat{\mu_{t, a}}\)에 상응하는 신뢰 구간 \(c_{t, a}\)를 \(|\hat{\mu_{t, a}} - \mu_a | < c_{t, a}\) 식이 높은 확률을 갖는 조건 하에 추정해낸다. 그런 다음 가장 높은 신뢰 상한(줄여서 UCB)을 갖는 슬롯 손잡이를 선택한다. 즉, \(a_t = argmax_a (\hat{\mu_{t, a}} + c_{t, a})\)이다. 적절히 정의한 신뢰 구간을 사용하면 해당 알고리즘 리그릿은 총 시도 횟수 \(T\)에 대해 단지 로그 수준으로 증가한다. 이는 최적으로 증명된 수준으로써 총 \(T\)번 시도에 대해 매우 작은 리그릿을 갖는다.

맥락 무관한, \(K\)개의 슬롯 손잡이를 갖는 다중 슬롯머신 실험의 경우 광범위하게 연구하면서 이해가 깊어졌지만 보다 일반적인 컨텍스츄얼 밴딧 문제는 여전히 난제이다. EXP4 알고리즘은 \(\tilde{O}(\sqrt{T})\)의 리그릿²을 달성하기 위해 지수 가중 기법을 이용하지만 변수 개수가 늘어남에 따라 계산 복잡도가 지수적으로 증가한다. 일반적인 컨텍스츄얼 밴딧 알고리즘 중 하나는 \(\epsilon\)을 축소시켜 나가는 \(\epsilon\)-탐욕과 비슷한 유형의 에폭 탐욕 알고리즘이다. 해당 알고리즘은 신탁적 옵티마이저가 주어진다는 가정 하에 계산 양이 효율적이지만 보장하는 리그릿은 \(\tilde{O}(T^{2 \over 3})\) 수준으로 약한 편이다.

다중 슬롯머신 실험에 대한 다양한 모형화 가정 아래 리그릿을 좀 더 강력히 보장하는 알고리즘을 설계할 수 있다. Auer는 슬롯 손잡이의 손익 기댓값이 변수에 선형적이라고 가정하고 본질적으로 UCB 유형의 접근법인 LinRel 알고리즘을 소개했다. 그 변형 중 하나는 이전 알고리즘을 상당히 개선하여 \(\tilde{O}(\sqrt{T})\)의 리그릿을 갖는다.

마지막으로 기틴스 지수 방법처럼 베이즈 법칙에 기반한, 또 다른 종류의 다중 슬롯머신 실험 알고리즘이 존재한다. 베이즈 접근법은 정의한 사전 분포가 적절한 경우 좋은 성능을 발휘한다. 이 방법은 적합한 사전 모형을 얻기 위해 오프라인 엔지니어링이 광범위하게 필요하며 근사 기법을 결합시키지 않으면 계산이 불가능하다.

3. 알고리즘

맥락 무관한 다중 슬롯머신 실험 알고리즘에 대한 UCB 방법의 점근적 최적성, 그리고 강력한 리그릿 수준을 감안할 때 컨텍스츄얼 밴딧 문제에 대해서도 유사한 알고리즘을 고려해볼 만하다. 손익 함수가 모수적 형태로 주어진다면 슬롯 손잡이 추정 손익의 UCB 계산을 위해 모수 신뢰 구간을 데이터로부터 추정해내는 수많은 방법이 존재한다. 그러나 이러한 접근법은 보통 계산 비용이 매우 높다.

본 연구는 손익 모형이 선형일 때 신뢰 구간을 닫힌 해를 통해 효율적으로 계산해낼 수 있음을 보인다. 그리고 해당 알고리즘을 LinUCB라고 부를 것이다. 편의를 위해 분리 선형 모형이라는 단순 형태를 먼저 설명하고 3.2절에서 혼합 모형이라는 더 일반적인 형태를 고려한다. LinUCB는 뉴스 기사 개인화 추천 이외의 응용 프로그램에 적용 가능한, 일반적인 컨텍스츄얼 밴딧 알고리즘이다.

3.1 분리 선형 모형을 이용한 LinUCB

2.1절의 표기법을 그대로 사용하겠다. 모든 \(t\)에 대하여 슬롯 손잡이 \(a\)의 손익 기댓값은 \(d\)-차원 변수 \(\mathbf{x}_t\)에 선형이며 미지의 계수 벡터 \(\boldsymbol{\theta}^*_a\)를 갖는다고 가정한다.

파라미터를 다른 슬롯 손잡이와 공유하지 않기 때문에 본 모형은 분리형이다. \(\mathbf{D}_a\)를 \(t\)번째 시도에서의 \(m \times d\) 차원인 설계 행렬이라고 정의하자. 행은 \(m\) 개의 훈련 입력값(예: 기사 \(a\)에 대해 이전 관측한 맥락 정보)에 해당하며 \(\mathbf{c}_a \in \mathbb{R}^m\)를 그에 상응하는 응답 벡터(예: 상응하는 \(m\) 개의 클릭 여부 사용자 피드백)라고 하자. 훈련 데이터 \((\mathbf{D}_a, \mathbf{c}_a)\)에 릿지 회귀 분석을 적용하면 계수 추정 값을 얻을 수 있다.

여기서 \(\mathbf{I}_d\)는 \(d \times d\) 차원인 항등 행렬이다. \(\mathbf{c}_a\)의 성분들이 \(\mathbf{D}_a\)의 상응하는 행에 대해 조건부 독립일 때, 임의의 \(\delta > 0\)와 \(\mathbf{x}_{t, a} \in \mathbb{R}^d\)에 대해 적어도 \(1 - \delta\)의 확률로

이다. 여기서 \(\alpha = 1 + \sqrt{\ln{(2/\delta)}/2}\)은 상수이다. 다시 말해서 위 부등식은 슬롯 손잡이 \(a\)의 손익 기댓값에 대해 엄밀한 UCB를 합리적으로 제공하며 이로부터 UCB 유형의 슬롯 손잡이 선택 전략이 파생될 수 있다. 각 \(t\)번째 시도에서

을 고른다. 식 (4)에서의 신뢰구간은 다른 원리를 적용해 계산해낼 수 있다. 예를 들자면 릿지 회귀는 베이즈 식의 점 추정으로 해석할 수 있는데 여기서 계수 벡터의 사후 분포 즉, \(p(\boldsymbol{\theta}_a)\)는 평균 \(\hat{\boldsymbol{\theta}}_a\)와 공분산 \(\mathbf{A}^{-1}_a\)를 갖는 정규분포이다. 모형이 주어졌을 때 손익 기댓값 \(\mathbf{x}^{\mathsf{T}}_{t, a}\boldsymbol{\theta}^*_a\)의 예측 분산은 \(\mathbf{x}^{\mathsf{T}}_{t, a}\mathbf{A}^{-1}_a\mathbf{x}_{t, a}\)으로, 표준편차는 \(\sqrt{\mathbf{x}^{\mathsf{T}}_{t, a}\mathbf{A}^{-1}_a\mathbf{x}_{t, a}}\)로 계산된다. 또한 정보 이론에서 \(p(\boldsymbol{\theta}_a)\)의 미분 엔트로피는 \(-{1 \over 2} \ln((2\pi)^d\det \mathbf{A}_a)\)로 정의된다. 점 \(\mathbf{x}_{t, a}\)이 새로 포함되어 갱신이 발생할 경우 \(p(\boldsymbol{\theta}_a)\)의 엔트로피는 \(-{1 \over 2} \ln((2\pi)^d\det (\mathbf{A}_a + \mathbf{x}_{t, a}\mathbf{x}^{\mathsf{T}}_{t, a}))\)가 된다. 사후 분포 모형의 엔트로피 감소분은 \(-{1 \over 2}\ln(1 + \mathbf{x}^{\mathsf{T}}_{t, a}\mathbf{A}^{-1}_a\mathbf{x}_{t, a})\)이다. \(\mathbf{x}_{t, a}\)이 모형을 개선하는데 기여한 정도를 계산할 때 이 양을 종종 사용한다. 따라서 식 (5)에서 슬롯 손잡이 선택 기준은 손익 추정과 모형 분산 감소 간의, 덧셈으로 연결된 트레이드오프 수준이라고 생각할 수 있다.

알고리즘 1은 입력 파라미터가 오직 \(\alpha\)인 LinUCB 알고리즘 전반에 대하여 자세하게 설명한다. 식 (4)에 표시한 \(\alpha\)를 보라. 일부 응용 프로그램에서는 보수적으로 큰 값을 취하기도 하는데 해당 파라미터를 최적화하면 전체 손익을 높일 수 있다. 모든 UCB 방법과 마찬가지로 LinUCB는 UCB가 가장 높은 슬롯 손잡이를 항상 선택한다(식 (5)와 같다).

이 알고리즘은 몇 가지 좋은 성질이 있다. 첫째, 계산 복잡도가 슬롯 손잡이 개수에 선형이며 변수 개수에 최대 세제곱이다. 계산량을 더 줄이기 위해 모든 단계(\(O(d^2)\) 시간이 걸리는)에서 \(\mathbf{A}_{a_t}\)를 실시간으로 업데이트하는 대신 주기적으로 \(\mathbf{Q}_a \overset{\underset{\mathrm{def}}{}}{=} \mathbf{A}^{-1}_{a_t}\) (모든 \(a\)에 대하여)를 계산하고 캐시 할 수 있다. 둘째, 알고리즘은 동적인 슬롯 손잡이 집합에 대해 잘 작동하며 \(\mathcal{A}_t\)의 크기가 너무 크지 않은 한 효율적이다. 이는 많은 응용 프로그램에 해당하는 경우이다. 예를 들어 뉴스 기사 추천의 경우 편집자가 기사를 풀에 추가 / 제거하기 때문에 본질적으로 풀의 크기는 일정하다. 셋째, 본 논문의 주안점은 아니지만 해당 논문³의 분석 결과를 다음과 같이 적용해볼 수 있다. 집합 \(\mathcal{A}_t\)가 고정되어 있고 슬롯 손잡이가 \(K\)개일 경우 데이터가 증가하면 신뢰 구간(즉, 식 (4)의 우항)이 충분히 빠르게 감소하며 강력한 리그릿 상한 \(\tilde{O}(\sqrt{KdT})\)을 갖는다. 이는 앞서 언급한 최신 논문 중 식 (2), 다중 슬롯머신 실험 결과에 부합한다. 본 이론적 결과는 알고리즘이 기본적으로 양질이며 효율적임을 나타낸다.

알고리즘 1 분리 선형 모형을 이용한 LinUCB

0: 입력: \(\alpha \in \Bbb{R}_+\)
1: for \(t = 1, 2, 3, \ldots , T\) do
2: \(\qquad\) 모든 슬롯 손잡이 \(a \in \mathcal{A}_t\)의 변수 \(\mathbf{x}_{t, a} \in \Bbb{R}_d\)를 관측함
3: \(\qquad\) for all \(a \in \mathcal{A}_t\) do
4: \(\qquad \qquad\) if \(a\)가 신규라면 then
5: \(\qquad \qquad \qquad \mathbf{A}_a \leftarrow \mathbf{I}_d\) (\(d\) 차원의 항등 행렬)
6: \( \qquad \qquad \qquad \mathbf{b}_a \leftarrow \mathbf{0}_{d \times 1}\) (\(d\) 차원의 영 벡터)
7: \(\qquad \qquad \) end if
8: \(\qquad \qquad \hat{\boldsymbol{\theta}}_a \leftarrow \mathbf{A}^{-1}_a\mathbf{b}_a \)
9: \(\qquad \qquad p_{t, a} \leftarrow \hat{\boldsymbol{\theta}}^{\mathsf{T}}_a\mathbf{x}_{t, a} + \alpha\sqrt{\mathbf{x}^{\mathsf{T}}_{t, a}\mathbf{A}^{-1}_a\mathbf{x}_{t, a}}\)
10: \(\qquad\) end for
11: \(\qquad\) 슬롯 손잡이 \(a_t = \arg\max_{a \in \mathcal{A}_t} p_{t, a}\)를 선택하되 동점인 경우 무작위로 정하고 실수 값 손익 \(r_t\)를 관측함
12: \(\qquad \mathbf{A}_{a_t} \leftarrow \mathbf{A}_{a_t} + \mathbf{x}_{t, a_t}\mathbf{x}^{\mathsf{T}}_{t, a_t}\)
13: \(\qquad \mathbf{b}_{a_t} \leftarrow \mathbf{b}_{a_t} + r_t\mathbf{x}_{t, a_t}\)
14: end for

마지막으로 입력 변수 \(\mathbf{x}_{t, a}\)를 정규분포에서 i.i.d.로 추출한다는 가정 하에서(식 (2)의 모형화 가정에 덧붙여) Palidis 등은 UCB를 계산하기 위해 릿지 회귀의 해(식 (3)의 \(\hat{\boldsymbol{\theta}}_a\)) 대신 최소 자승 해 \(\tilde{\boldsymbol{\theta}}_a\)를 이용한 유사 알고리즘을 제안했다. 그러나 본 접근법(그리고 이론적 분석)이 보다 일반적이며 입력 변수가 정상(stationary) 상태가 아닐 경우에도 유효하다. 보다 중요하게 기본 알고리즘 1을 Pavlidis 등이 다루지 않은, 훨씬 더 흥미로운 경우로 확장하는 방법에 관해 다음 절에서 논할 것이다.

3.2 혼합 선형 모형을 이용한 LinUCB

알고리즘 1(또는 해당 논문³과 유사한 알고리즘)은 행렬 \(\mathbf{D}^{\mathsf{T}}_a\mathbf{D}_a + \mathbf{I}_d\)(또는 \(\mathbf{D}^{\mathsf{T}}_a\mathbf{D}_a\))의 역행렬을 계산한다. 여기서 \(\mathbf{D}_a\)는 학습 데이터 변수에 해당하는 행을 갖는 설계 행렬이다. 슬롯 손잡이의 모든 행렬은 고정된 차원 \(d \times d\)를 가지며 업데이트를 점진적, 효율적으로 수행할 수 있다. 또한 알고리즘 1의 파라미터는 상호 분리되어 있기 때문에 역행렬을 쉽게 계산할 수 있다. 식 (3) 중 \(\hat{\boldsymbol{\theta}}_a\)는 다른 슬롯 손잡이가 갖는 훈련 데이터의 영향을 받지 않으므로 별도 계산할 수 있다. 이제 혼합 모형이라는 더 재밌는 사례를 살펴보자.

응용 프로그램 다수의 경우 특정 슬롯 손잡이 변수에 더하여 모든 슬롯 손잡이가 공유하는 변수를 사용하는 편이 선호된다. 예를 들자면 어떤 사용자는 정치 기사만 선호할 수 있고 뉴스 기사 추천은 이에 대한 메커니즘을 제공할 수 있다. 따라서 공유 또는 비공유 구성 요소가 함께 있는 변수를 갖는 편이 좋다. 식 (2) 우항에 또 다른 선형 항을 추가한 다음의 혼합 모형을 채택하자.

여기서 \(\mathbf{z}_{t, a} \in \Bbb{R}^k\)는 특정 사용자 / 기사 조합의 변수이고 \(\boldsymbol{\beta}^*\)는 모든 슬롯 손잡이 공통의 알려지지 않은 계수 벡터이다. 계수 \(\boldsymbol{\beta}^*\) 중 일부는 모든 슬롯 손잡이에 의해 공유되는 반면 \(\boldsymbol{\theta}^*_a\)는 그렇지 않다는 점에서 본 모형은 혼합이다.

혼합 모형의 경우 슬롯 손잡이 다수의 신뢰 구간이 공유 변수로 인해 독립이 아니므로 알고리즘 1을 더 이상 사용할 수 없다. 다행히 이전 절의 추론을 동일하게 따라가며 UCB를 계산하는 효율적 방법이 있다. 식의 전개는 블록 행렬의 역을 구하는 기법에 크게 의존한다. 지면 상 제약으로 알고리즘 2에서는 의사 코드만 제시하겠다(5와 12행은 계수의 릿지 회귀 해를 계산하고 13행은 신뢰 구간을 계산함). 상세한 전개식은 정식 논문에 적어둔다. 알고리즘을 구성하는 블록들(\(\mathbf{A}_0, \mathbf{b}_0, \mathbf{A}_a, \mathbf{B}_a\)와 \(\mathbf{b}_a\))의 차원은 모두 고정된 크기이며 점진적 업데이트 수행 또한 가능하므로 본 알고리즘은 계산 효율적이다. 그리고 \(\mathcal{A}_t\)에서 제거된 슬롯 손잡이와 관련된 수치는 더 이상 계산에 사용되지 않는다. 마지막으로 모든 시행마다 계산하는 대신 역행렬들(\(\mathbf{A}^{-1}_0\)와 \(\mathbf{A}^{-1}_a)\)을 주기적으로 계산하고 캐시 하면 시행 당 계산 복잡도를 \(O(d^2 + k^2)\)로 줄일 수 있다.

알고리즘 2 혼합 선형 모형을 이용한 LinUCB

0: 입력: \(\alpha \in \Bbb{R}_+\)
1: \(\mathbf{A}_0 \leftarrow \mathbf{I}_k\) (\(k\)차원의 항등 행렬)
2: \(\mathbf{b}_0 \leftarrow \mathbf{0}_k\) (\(k\)차원의 영 벡터)
3: for \(t = 1, 2, 3, \ldots , T\) do
4: \(\qquad\) 모든 슬롯 손잡이 \(a \in \mathcal{A}_t\)의 변수 (\(\mathbf{z}_{t, a}, \mathbf{x}_{t, a} \in \Bbb{R}^{k + d}\))를 관측함
5: \(\qquad \hat{\boldsymbol{\beta}} \leftarrow \mathbf{A}^{-1}_0\mathbf{b}_0\)
6: \(\qquad \) for all \(a \in \mathcal{A}_t\) do
7: \(\qquad \qquad\) if \(a\)가 신규라면 then
8: \(\qquad \qquad \qquad \mathbf{A}_a \leftarrow \mathbf{I}_d\) (\(d\) 차원의 항등 행렬)
9: \(\qquad \qquad \qquad \mathbf{B}_a \leftarrow \mathbf{I}_{d \times k}\) (\(d \times k\) 차원의 영 행렬)
10: \( \qquad \qquad \qquad \mathbf{b}_a \leftarrow \mathbf{0}_{d \times 1}\) (\(d\) 차원의 영 벡터)
11: \(\qquad \qquad \) end if
12: \(\qquad \qquad \hat{\boldsymbol{\theta}}_a \leftarrow \mathbf{A}^{-1}_a\left(\mathbf{b}_a - \mathbf{B}_a\hat{\boldsymbol{\beta}}\right)\)
13: \(\qquad \qquad s_{t, a} \leftarrow \mathbf{z}^{\mathsf{T}}_{t, a}\mathbf{A}^{-1}_0\mathbf{z}_{t, a} - 2\mathbf{z}^{\mathsf{T}}_{t, a}\mathbf{A}^{-1}_0\mathbf{B}^{\mathsf{T}}_a\mathbf{A}^{-1}_a\mathbf{x}_{t, a} + \mathbf{x}^{\mathsf{T}}_{t, a}\mathbf{A}^{-1}_a\mathbf{x}_{t, a} + \mathbf{x}^{\mathsf{T}}_{t, a}\mathbf{A}^{-1}_a\mathbf{B}_a\mathbf{A}^{-1}_0\mathbf{B}^{\mathsf{T}}_a\mathbf{A}^{-1}_a\mathbf{x}_{t, a}\)
14: \(\qquad \qquad p_{t, a} \leftarrow \mathbf{z}^{\mathsf{T}}_{t, a}\hat{\boldsymbol{\beta}} + \mathbf{x}^{\mathsf{T}}_{t, a}\hat{\boldsymbol{\theta}}_a + \alpha\sqrt{s_{t, a}}\)
15: \(\qquad \) end for
16: \(\qquad\) 슬롯 손잡이 \(a_t = \arg\max_{a \in \mathcal{A}_t} p_{t, a}\)를 선택하되 동점인 경우 무작위로 정하고 실수 값 손익 \(r_t\)를 관측함
17: \(\qquad \mathbf{A}_0 \leftarrow \mathbf{A}_0 + \mathbf{B}^{\mathsf{T}}_{a_t}\mathbf{A}^{-1}_{a_t}\mathbf{B}_{a_t} \)
18: \(\qquad \mathbf{b}_0 \leftarrow \mathbf{b}_0 + \mathbf{B}^{\mathsf{T}}_{a_t}\mathbf{A}^{-1}_{a_t}\mathbf{b}_{a_t} \)
19: \(\qquad \mathbf{A}_{a_t} \leftarrow \mathbf{A}_{a_t} + \mathbf{x}_{t, a_t}\mathbf{x}^{\mathsf{T}}_{t, a_t}\)
20: \(\qquad \mathbf{B}_{a_t} \leftarrow \mathbf{B}_{a_t} + \mathbf{x}_{t, a_t}\mathbf{z}^{\mathsf{T}}_{t, a_t}\)
21: \(\qquad \mathbf{b}_{a_t} \leftarrow \mathbf{b}_{a_t} + r_t\mathbf{x}_{t, a_t}\)
22: \(\qquad \mathbf{A}_0 \leftarrow \mathbf{A}_0 + \mathbf{z}_{t, a_t}\mathbf{z}^{\mathsf{T}}_{t, a_t} - \mathbf{B}^{\mathsf{T}}_{a_t}\mathbf{A}^{-1}_{a_t}\mathbf{B}_{a_t} \)
23: \(\qquad \mathbf{b}_0 \leftarrow \mathbf{b}_0 + r_t\mathbf{z}_{t, a_t} - \mathbf{B}^{\mathsf{T}}_{a_t}\mathbf{A}^{-1}_{a_t}\mathbf{b}_{a_t}\)
24: end for

4. 평가 방법론

지도 학습 상황에서 진행하는 보다 표준화된 기계 학습과 비교하자면 컨텍스츄얼 밴딧을 위한 평가 방법론은 꽤나 까다롭다. 밴딧 알고리즘 \(\pi\), 즉 앞서 발생한 상호 작용을 기반으로 각 시점마다 슬롯 손잡이를 선택하는 규칙(예컨대 위에서 설명한 알고리즘)의 성능을 측정하는 것이 목표이다. 그러나 상호 작용적인 특성 때문에 “라이브” 데이터 위에서 알고리즘을 실제 수행해보는 것 외에 목표를 달성할 방법이 없어보인다. 서비스에 들어갈 비용을 생각하면 이런 접근법은 사실상 실행 불가능하다. 지금 알고리즘과는 완전히 다른 예전의 로깅 정책을 사용해 수집한 오프라인 데이터만 이용 가능하다. 로깅 정책에 의해 선택된 슬롯 손잡이에서의 결과 값만 관측되며 이는 평가 대상 알고리즘 \(\pi\)에 의해 선택될 슬롯손잡이의 결과 값과 매우 다를 것이다. 그렇기에 기존 로깅 데이터에 의존해서 어떻게 \(\pi\)를 평가할 수 있을지 명확하지 않다. 이 평가 문제는 강화 학습에서의 “오프-폴리시 평가”의 특수한 경우로 볼 수 있다(해당 논문⁴를 참조하라). 지도 학습 상황에서 진행하는 보다 표준화된 기계 학습과 비교하자면 컨텍스츄얼 밴딧을 위한 평가 방법론은 꽤나 까다롭다. 밴딧 알고리즘 \(\pi\), 즉 앞서 발생한 상호 작용을 기반으로 각 시점마다 슬롯 손잡이를 선택하는 규칙(예컨대 위에서 설명한 알고리즘)의 성능을 측정하는 것이 목표이다. 그러나 상호 작용적인 특성 때문에 “라이브” 데이터 위에서 알고리즘을 실제 수행해보는 것 외에 목표를 달성할 방법이 없어 보인다. 서비스에 들어갈 비용을 생각하면 이런 접근법은 사실상 실행 불가능하다. 지금 알고리즘과는 완전히 다른 예전의 로깅 정책을 사용해 수집한 오프라인 데이터만 이용 가능하다. 로깅 정책에 의해 선택된 슬롯 손잡이에서의 결과 값만 관측되며 이는 평가 대상 알고리즘 \(\pi\)에 의해 선택될 슬롯 손잡이의 결과 값과 매우 다를 것이다. 그렇기에 기존 로깅 데이터에 의존해서 어떻게 \(\pi\)를 평가할 수 있을지 명확하지 않다. 이 평가 문제는 강화 학습에서의 “오프-폴리시 평가”의 특수한 경우로 볼 수 있다(해당 논문⁴를 참조하라).

한 가지 해결책은 로깅 데이터로부터 밴딧의 절차를 모형화하기 위해 시뮬레이터를 구축한 다음 시뮬레이터로 \(\pi\)를 평가하는 것이다. 그러나 모형 작업은 시뮬레이터에 편향을 가져오므로 시뮬레이터 기반 평가 방식의 신뢰성은 증명하기 어렵다. 그보다 구현하기 쉽고 로깅 데이터에 근거하는, 편향 없는 방법론을 제안한다.

개별 이벤트는 i.i.d.이고 로깅 데이터를 수집하는 데 사용된 로깅 정책은 각 시점마다 슬롯 손잡이를 무작위로 균일하게 선택했다고 가정하자. 해당 가정 하에 평가를 수행하는 신뢰도 높은 기법을 이 장에서 설명하겠다. 세부적인 내용은 생략하겠지만 임의의 로깅 정책이 허용되게끔 후자의 가정을 약화시킬 수 있다. 또한 본 해법이 리젝션 샘플링을 사용하게끔 변경할 수 있으나 그럴 경우 데이터 사용의 효율이 떨어진다.

보다 정확하게 \((\mathbf{x}_1, \ldots, \mathbf{x}_K, r_1, \ldots, r_K)\) 형태의, 즉 관측한 변수 벡터와 모든 슬롯 손잡이에 대해 감춰진 손익으로 구성한 튜플을 i.i.d.로 추출 가능한 미지의 분포 \(D\)가 있다고 가정하자. 그리고 로깅 정책과 현실 세계 간의 상호 작용으로 발생한 대량의 이벤트 로그를 이용할 수 있다고 하자. 각각의 이벤트는 맥락 벡터 \(\mathbf{x}_1, \ldots, \mathbf{x}_K\), 선택한 슬롯 손잡이 \(a\)와 그에 따라 관측한 손익 \(r_a\)로 구성된다. 중요한 건 무작위로 균일하게 선택한 단일 슬롯 손잡이 \(a\)에 대응하는 손익 \(r_a\)만 관측된다는 사실이다. 단순한 표현을 위해 이벤트 로그의 순열을 무한히 긴 스트림 형태라고 가정하자. 그러나 평가 방법론에 사용할, 실제로는 유한한 건수의 이벤트에 대해서도 명시적인 수치를 제시할 것이다.

목표는 해당 데이터를 사용하여 밴딧 알고리즘 \(\pi\)를 평가하는 것이다. 공식적으로 \(\pi\)는 현시점의 맥락 벡터\(\mathbf{x}_1, \ldots, \mathbf{x}_K\)와 함께 \(t-1\)개의 이전 시점 이력 \(h_{t-1}\)을 기반으로 현시점 \(t\)에서 슬롯 손잡이를 선택하는 (무작위성이 가미된) 연결 논리이다.

본 논문에서 제안하는 정책 평가자는 알고리즘 3에 나와있다. 이 방법론은 정책 \(\pi\)와 평가의 기초인 “양질의” 이벤트에 대해 필요한 건수 \(T\)를 입력으로 취한다. 그런 다음 이벤트 로그 스트림을 하나씩 살펴본다. 주어진 현재 이력 \(h_{t-1}\)에 대해 정책 \(\pi\)가 선택한 슬롯 손잡이 \(a\)가 로깅 정책에 의해 선택한 것과 동일하면 발생 이벤트는 보존한다. 즉, 이력에 추가하고 총 손익 \(R_t\)을 업데이트한다. 반대로 정책 \(\pi\)가 선택한 슬롯 손잡이가 로깅 정책에 의해 취한 것과 다르면 발생 이벤트는 무시하고 알고리즘은 상태의 변경 없이 다음 이벤트로 진행된다.

알고리즘 3 정책 평가자

0: 입력: \(T > 0\); 정책 \(\pi\); 이벤트 스트림
1: \(h_0 \leftarrow \varnothing\) {초기의 빈 이력}
2: \(R_0 \leftarrow 0\) {초기 0 값의 총 손익}
3: for \(t = 1, 2, 3, \ldots, T\) do
4: \(\qquad\) repeat
5: \(\qquad \qquad\) 다음 이벤트 \((\mathbf{x}_1, \ldots, \mathbf{x}_K, a, r_a)\)을 취함
6: \(\qquad\) until \(\pi(h_{t-1}, (\mathbf{x}_1, \ldots, \mathbf{x}_K)) = a\)
7: \(\qquad h_t \leftarrow CONCATENATE(h_{t-1}, (\mathbf{x}_1, \ldots, \mathbf{x}_K, a, r_a))\)
8: \(\qquad R_t \leftarrow R_{t-1} + r_a\)
9: end for
10: 출력: \(R_T / T\)

로깅 정책은 각 슬롯 손잡이를 균일하게 무작위 선택하기 때문에 정책 평가자를 거치는 동안 각 이벤트의 발생 확률은 정확히 \(1 / K\)를 독립적으로 유지한다. 이는 보존한 이벤트가 \(D\)에 의해 선택된 것과 동일한 분포를 가짐을 뜻한다. 결과적으로 두 절차가 동일함을 증명할 수 있다. 여기서 두 절차란 전자는 \(D\)로부터 발생한 \(T\) 건의 실제 이벤트에 대해 정책을 평가함을, 후자는 이벤트 로그 스트림에서 정책 평가자를 적용하여 정책을 평가함을 뜻한다.

정리 1. 맥락에 대한 모든 분포 \(D\), 모든 정책 \(\pi\), 모든 \(T\) , 모든 이벤트의 순서 \(h_T\)에 대하여,

여기서 \(S\)는 균일하게 무작위 선택하는 로깅 정책과 \(D\)로부터 i.i.d.로 추출한 이벤트 스트림이다. 덧붙여 \(T\)건의 이력 \(h_T\)을 모으기 위해 스트림에서 추출할 이벤트의 기대 건수는 \(KT\)이다.

정책 평가자 내의 모든 이력 \(h_T\)가 현실 세계에서 발생할 확률과 동일하다고 이 정리는 이야기한다. 알고리즘 3이 반환하는 평균 손익 \(R_T / T\)처럼 이력에 관한 다수의 통계량은 알고리즘 \(\pi\)에 대한 편향되지 않은 추정치이다. 또한 정리에 따르면 \(T\)건의 관측치를 보유하기 위해 \(KT\)건의 이벤트 로그가 평균적으로 필요하다.

증명. 증명은 두 가지 평가 방법 모두에서 \(t = 0\) 시점의 발생 확률이 1인 빈 이력, 즉 기본 사례로 시작하여 \(t = 1, \ldots, T\) 순으로 귀납법을 적용하는 식이다. 귀납적 사례를 위해 모든 \(t − 1\) 시점에서 다음을 가정하자.

이제 모든 이력 \(h_t\)에 대해 동일 내용을 증명하고 싶다. 데이터는 i.i.d.이고 정책의 무작위성은 현실 세계의 무작위 선택과 독립이므로 이력 \(h_{t-1}\)이 주어졌을 때 \(t\) 번째 이벤트에 대한 분포가 절차 양쪽에서 동일하다는 걸 증명하면 된다. 즉, 다음을 보여야 한다.

로깅 정책은 슬롯 손잡이 \(a\)를 균일하게 무작위 선택하므로 정책 평가자가 내부 반복문에서 빠져나갈 확률은 모든 정책, 로그, 변수와 슬롯 손잡이에 대해 마지막 이벤트가 발생할 확률 \(\Pr_{D} (\mathbf{x}_{t, 1}, \ldots, \mathbf{x}_{t, K}, r_{t, a})\)로 동일하다. 마찬가지로 정책 \(\pi\)의 슬롯 손잡이에 대한 분포는 이력 \(h_{t-1}\)과 \((\mathbf{x}_{t, 1}, \ldots, \mathbf{x}_{t, K})\)에 대해 독립이므로 슬롯 손잡이 \(a\)의 확률은 단지 \(\Pr_{\pi(h_{t-1})}(a \mid \mathbf{x}_{t, 1}, \ldots, \mathbf{x}_{t, K})\)이다.

마지막으로 스트림의 각 이벤트는 정확히 \(1 / K\)의 확률로 보존되므로 \(T\)건의 이벤트를 보유하는데 필요한 기대 건수는 정확히 \(KT\)이다.

5. 실험

이 장에서는 4장의 오프라인 평가 방법을 사용하여 제안된 LinUCB 알고리즘의 역량을 애플리케이션 실적용을 통해 확인하겠다. 먼저 Yahoo! Today Module의 문제 설정을 소개한 다음 실험에 사용한 사용자 / 품목 변수를 설명하겠다. 마지막으로 성능 지표를 정의하고 몇 가지 표준 (컨텍스츄얼) 밴딧 알고리즘과 비교해가며 실험 결과를 제시하겠다.

5.1 Yahoo! Today Module

Today Module은 Yahoo! 앞단 페이지 중 가장 눈에 띄는 패널이며 가장 많이 방문하는 인터넷 페이지 중 하나이다. 그림 1의 스냅숏을 참조하라. Today Module의 “추천” 기본 탭은 양질의 기사 4개 중 하나(주로 뉴스)를 강조 표시한다. 이 4개의 기사는 편집자가 시간 단위로 선별하는 기사 풀에서 선택한다. 그림 1에 나와있는 것처럼 바닥 글 위치에 F1–F4로 색인화한 4개의 기사가 있다. 각 기사는 작은 그림과 제목으로 표시된다. 4개의 기사 중 하나가 스토리 위치에서 강조 표시되며 관련 링크와 함께 큰 그림, 제목 그리고 짧은 요약이 게시된다. 기본적으로 F1 기사가 스토리 위치에서 강조 표시된다. 기사에 관심이 있는 경우 스토리 위치에 강조 표시된 기사를 클릭하면 자세한 내용을 읽을 수 있다. 해당 이벤트는 스토리 클릭으로 기록된다. 방문자의 주목을 끌기 위해 개별 관심사에 따라 사용 가능한 기사의 순위를 매기고 스토리 위치에 각 방문자가 가장 흥미 있을 기사를 강조, 노출하고 싶다.

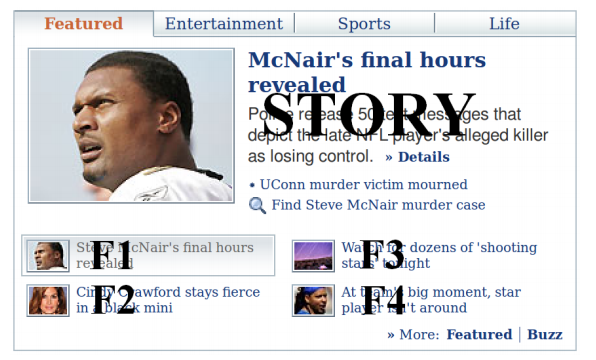그림 1: Yahoo!의 Today Module에서 “추천” 탭의 스냅숏 첫 페이지. 기본적으로 F1 위치의 기사는 스토리 위치에서 강조 표시된다.

5.2 실험 설정

아래 절에서 데이터 수집, 변수 구성, 성능 평가와 비교 알고리즘을 포함한 실험 설정 전반에 대한 자세한 설명을 하겠다.

5.2.1 데이터 수집

2009년 5월에 임의화 버킷에서 사건을 수집했다. 방문 보기마다 특정 확률로 사용자를 해당 버킷에 무작위 배정하였다.⁵ 해당 버킷은 사용자 서비스를 위해 기사 풀에서 기사를 임의로 선택했다. 바닥 글 위치에서의 노출 편향을 피하기 위해 스토리 위치 내 F1 기사와 사용자 간의 상호 작용에만 초점을 맞췄다. 사용자 별 상호 작용 이벤트는 (i) 사용자 서비스 제공을 위해 선택한 무작위 기사, (ii) 사용자 / 기사 정보 (iii) 스토리 위치에서 기사를 클릭하는지 여부로 구성된다. 이러한 임의의 이벤트로 밴딧 알고리즘 기대 손익을 신뢰성 있게 평가할 수 있다는 걸 4장에서 보였다.

5월 1일 임의화 버킷에 약 470만 건의 이벤트가 있었다. 모형 검증을 위해 이 날의 이벤트(“조정 데이터”라고 함)를 이용했고 각 비교 밴딧 알고리즘마다 최적 파라미터를 결정했다. 그런 다음 5월 3일부터 9일까지 임의화 버킷에서 1주일 간 모은 이벤트 집합(“평가 데이터”라고 함)에 대해 조정한 파라미터를 적용하여 알고리즘을 수행했다.

5.2.2 변수 구성

이제 실험을 위해 구성한 사용자 / 기사 변수에 대해 설명하겠다. 3장에서의 LinUCB 두 가지 형태를 실험하고 혼합 모형이 학습 속도를 향상할 수 있다는 가설을 검증하기 위해 분리 모형, 혼합 모형 각각을 위해 두 종류의 변수 집합을 사용했다.

원천 사용자 변수를 “지지도”로 거르고 시작하자. 변수의 지지도란 해당 변수를 갖는 사용자의 비율이다. 데이터의 잡음을 줄이기 위해 높은 지지도를 갖는 변수만 선택했다. 구체적으로 지지도 0.1 이상인 변수만 사용했다. 그런 다음 각 사용자를 1,000개가 넘는 범주형 구성 요소의 원천 변수 벡터로 표현했다. 이는 다음 내용을 포함한다. (i)

인구 통계학적 정보: 성별(2개의 범주)과 연령을 이용해 10개 세그먼트로 구분했다. (ii) 지리적 변수: 전 세계 또는 미국 주의 약 200곳 대도시, 그리고 (iii) 행위 유형: Yahoo! 내 사용자 콘텐츠 소비 기록을 요약한 약 1,000개의 이진 범주 변수. 이 변수들 외에 사용자를 식별하는데 다른 정보는 사용하지 않았다.

비슷하게 각 기사는 동일한 방식으로 구성한 범주형 변수 약 100개의 원천 변수 벡터로 표현하였다. (i) URL 범주: 기사 출처 URL에서 유추한 수십 개의 범주 (ii) 편집자 범주: 기사 내용을 요약하기 위해 편집자가 손수 태그를 붙이는 주제 수십 개.

선행 연구의 절차⁶에 따라 범주형 사용자 / 기사 변수를 이진 벡터로 인코딩한 다음 각 변수 벡터를 단위 벡터 크기로 정규화했다. 또한 각 변수 벡터에 대해 상수 변수 값 1을 덧붙였다. 결과적으로 기사와 사용자를 각각 83과 1,193개의 변수 벡터로 표현했다.

이러한 원천 변수를 사용하여 2008년 9월에 수집한 무작위 탐색 데이터를 기반으로 공동 분석을 수행했다. 선행 연구⁷의 차원 축소 접근법에 따라 사용자 변수를 기사 범주에 투영시킨 다음 유사 선호도를 가진 사용자를 집단으로 묶었다. 더 구체적으로,

• 먼저 로지스틱 회귀 분석(LR)을 사용하여 원천 사용자 / 기사 변수가 주어졌을 때의 클릭 확률에 대해 이중 선형 모형을 적합시켰다. 즉, \(\boldsymbol{\phi}^T_u\mathbf{W}\boldsymbol{\phi}_a\)를 사용자 \(u\)가 기사 \(a\)를 클릭할 확률로 근사 시켰고 이때 \(\mathbf{W}\)는 LR에 의해 최적화한 가중치 행렬이다.

• 그런 다음 원천 사용자 변수를 유도된 공간에 투영하여 \(\boldsymbol{\psi}_u \overset{\underset{\mathrm{def}}{}}{=} \boldsymbol{\phi}^T_u\mathbf{W}\)를 계산했다. 여기서 사용자 \(u\)에 대한 \(\boldsymbol{\psi}_u\)의 \(i^{th}\) 성분은 사용자가 기사의 \(i^{th}\) 범주를 좋아하는 정도로 해석할 수 있다. 유도된 \(\boldsymbol{\psi}_u\) 공간에서 사용자를 5개의 군집으로 묶기 위해 \(K\)-평균 군집화 알고리즘을 사용했다.

• 최종 사용자 변수는 6차원 벡터이다. 처음 5개의 항목은 해당 사용자가 5개의 군집(가우시안 커널로 계산한 다음 합쳐서 1이 되도록 정규화함)에 각각 속할 확률에 해당하며 6번째는 상수 변수 1이다.

\(t\) 시점에서 기사 \(a\)는 별도의 6차원 변수 \(\mathbf{x}_{t, a}\)을 가지며 이는 사용자 \(u_t\)와 정확히 동일하게, 상기한 절차로 구성한 6차원 변수이다. 이 기사 변수는 서로 겹치지 않기에 3장에서 정의한 분리 선형 모형을 위한 것이다.

각 기사 \(a\)마다 6차원의 기사 변수(상수 변수 1 포함)를 얻기 위해 동일한 차원 축소를 수행했다. 사용자 변수를 적용한 외적은 식 (6)의 공유 변수에 해당하며 \(\mathbf{z}_{t, a} \in \mathbb{R}^{36}\)로 표기하는 \(6 \times 6 = 36\)개의 변수를 제공한다. 따라서 \((\mathbf{z}_{t, a}, \mathbf{x}_{t, a})\)는 혼합 선형 모형에서 사용할 수 있다. \(\mathbf{z}_{t, a}\) 변수는 사용자-기사의 상호 작용 정보를 포함하고 \(\mathbf{x}_{t, a}\)는 사용자 정보만 포함한다.

여기서 선행한 세분화 분석⁷에서 대표적으로 나타난 5개의 사용자(및 기사) 군집을 의도적으로 사용했다. 상대적으로 작은 변수 공간을 사용하는 또 다른 이유는 온라인 서비스에서 대량의 사용자 / 기사 정보를 저장하고 검색하는 것은 너무 비용이 커서 실용적이지 않기 때문이다.

5.3 비교 알고리즘

실험에서 실증적으로 평가한 알고리즘은 세 집단으로 분류할 수 있다.

I. 변수를 사용하지 않는 알고리즘. 이들은 모든 맥락(예: 사용자 / 기사 정보)을 무시하는, 슬롯 손잡이 \(K\)개를 갖는 맥락 무관한 밴딧 알고리즘에 해당한다.

• 무작위: 무작위 정책은 풀의 기사 후보 중 하나를 항상 일정한 확률로 선택한다. 이 알고리즘은 파라미터를 필요로 하지 않고 시간에 따른 “학습”을 수행하지 않는다.
• \(\epsilon\)-탐욕: 2.2절에 설명한 대로 각 기사의 CTR을 추정한다. 그런 다음 \(\epsilon\)의 확률로 기사를 무작위 선택하고 \(1 - \epsilon\)의 확률로 CTR 추정치가 가장 높은 기사를 선택한다. 이 정책의 유일한 파라미터는 \(\epsilon\)이다.
• ucb: 2.2절에서 설명한 대로 이 정책은 각 기사 CTR 추정치의 신뢰 구간을 추정하고 UCB가 가장 높은 기사를 항상 선택한다. 특히 UCB1의 경우 기사 \(a\)의 신뢰 구간을 \(c_{t, a} = {\alpha \over \sqrt{n_{t, a}}}\)로 계산한다. 여기서 \(n_{t, a}\)는 \(t\) 시점 이전 \(a\)를 선택한 횟수이며 \(α > 0\)은 파라미터이다.
• 전지(全知)적: 이 정책은 맥락 무관한 CTR의 최고 통계치를 사후 평가로 계산한다. 즉, 이벤트 로그로부터 각 기사의 CTR 통계치를 먼저 계산한 다음 동일한 이벤트 로그를 이용하여 CTR 통계치가 가장 높은 기사를 무조건 선택한 후 평가한다. 이 알고리즘은 파라미터가 필요하지 않으며 시간에 따른 “학습”을 수행하지 않는다.

II. “웜 스타트”를 적용한 알고리즘. - 개인화 서비스를 향한 중간 단계. 아이디어는 전체 트래픽으로 구한, 기사의 맥락 무관한 CTR에 대해 오프라인에서 예측한 사용자 별 조정 값을 제공하는 것이다. 오프셋은 신규 콘텐츠에 대한 CTR 추정치의 초기값, 말하자면 “웜 스타트” 역할을 한다. 위에서 구성한 변수 \(\mathbf{z}_{t, a}\)를 이용하여 2008년 9월의 무작위 트래픽 데이터에 대해 선행 논문⁶에서 연구했던 이중 선형 로지스틱 회귀 모형을 재훈련시켰다. 그러면 선택 기준은 맥락 무관한 CTR 추정치와 사용자 별 CTR 조정을 위한 이중 선형 항의 합계가 된다. 모형 훈련의 경우 \(\epsilon = 1\)인 맥락 무관 한 \(\epsilon\)-탐욕을 사용하여 CTR을 추정했다.

• \(\epsilon\)-탐욕(웜 스타트): 이 알고리즘은 기사의 맥락 무관한 CTR 추정치에 사용자 별 CTR 조정을 추가한다는 점을 제외하면 \(\epsilon\)-탐욕과 동일하다.
• ucb(웜 스타트): 본 알고리즘은 바로 위 알고리즘과 동일하되 \(\epsilon\)-탐욕만 ucb로 대체한다.

III. 온라인에서 사용자 별 CTR을 학습하는 알고리즘.

• \(\epsilon\)-탐욕(세분화): 각 사용자를 5.2.2절에서 구성한 5개의 사용자 군집 중 가장 가까운 것에 배정해서 모든 사용자를 5개의 집단(즉, 사용자 세그먼트)으로 분할한다. 각 집단마다 별도의 \(\epsilon\)-탐욕 사본을 실행한다.
• ucb(세분화): 본 알고리즘은 5개의 사용자 세그먼트 각각마다 ucb의 복사본을 실행하는 것을 빼고는 \(\epsilon\)-탐욕(세분화)와 동일하다.
• \(\epsilon\)-탐욕(분리): 분리 선형 모형을 사용한 \(\epsilon\)-탐욕이며 에폭 탐욕과 밀접한 변종으로 볼 수 있다.
• linucb(분리): 분리 선형 모형을 사용한 알고리즘 1이다.
• \(\epsilon\)-탐욕(혼합): 혼합 선형 모형을 사용한 \(\epsilon\)-탐욕이며 에폭 탐욕과 밀접한 변종으로 볼 수 있다.
• linucb(혼합): 혼합 선형 모형을 사용한 알고리즘 2이다.

5.4 성능 지표

알고리즘의 클릭률은 클릭 건수를 노출 단계가 실행된 건수로 나눈 비율로 정의한다. 각 알고리즘마다 무작위 이벤트 로그에 대한 CTR을 측정해 성능 비교 기준으로 삼았다. 비즈니스 민감 정보를 보호하기 위해 각 알고리즘 CTR을 무작위 정책의 CTR로 나눠 알고리즘의 상대적 CTR만 표시하겠다. 따라서 무작위 정책의 상대적 CTR은 정의에 의해 항상 1이므로 따로 표시하지 않겠다. 편의상 “상대적 CTR” 대신 “CTR”이라는 용어를 사용한다.

본 응용 프로그램에서 아이디어를 얻은 두 종류의 CTR이 각 알고리즘의 관심 대상이다. 해당 개념은 다른 응용 프로그램에서도 유용할 수 있다. 모형을 Yahoo!의 첫 페이지에 배포하기 위한 합리적인 접근법 중 하나는 해당 페이지의 전체 트래픽을 두 개의 버킷에 무작위 배분하는 것이다. 전자의 “학습 버킷”은 일반적으로 기사 CTR을 학습 / 추정하기 위해 다양한 밴딧 알고리즘을 실행하는 소량의 트래픽으로 구성한다. 후자의 “배포 버킷”은 학습 버킷에서 얻은 CTR 추정치를 사용하여 사용자에게 탐욕적으로 Yahoo! Front Page 서비스를 제공한다. 본 문제의 경우 “학습”과 “배포”가 연동되므로 배포 버킷으로 배분되는 모든 보기마다 현재 (사용자 별) CTR 추정치가 가장 높은 기사를 선택해 보여준다. 학습 버킷에 더 많은 데이터가 들어오면 해당 추정치는 향후 변경될 수 있다. 버킷 양쪽의 CTR 모두 알고리즘 3으로 추정했다.

배포 버킷은 종종 학습 버킷보다 크기 때문에 배포 버킷의 CTR이 더 중요하다. 그러나 학습 버킷에서 CTR이 높다는 건 해당 밴딧 알고리즘의 학습 속도가 더 빠름(동치로 리그릿이 더 작음)을 의미한다. 따라서 버킷 양쪽의 알고리즘 CTR을 제시하겠다.

5.5 실험 결과

5.5.1 조정 데이터에 대한 결과

5.3절에 나온 비교 알고리즘(무작위와 전지적 정책 제외)은 모두 조정해야 할 파라미터가 한 개씩 있다. \(\epsilon\)-탐욕 알고리즘의 경우 \(\epsilon\), UCB 알고리즘의 경우 \(\alpha\)이다. 이 파라미터를 최적화하기 위해 조정 데이터를 사용했다. 그림 2는 각 알고리즘의 CTR이 파라미터 별로 어떻게 변하는지 보여준다. 모든 결과는 단일 실행으로 얻은 것이지만 데이터셋 크기와 정리 1에 나온 불편성 결과를 고려할 때 표시된 값은 통계적으로 신뢰할 수 있다.

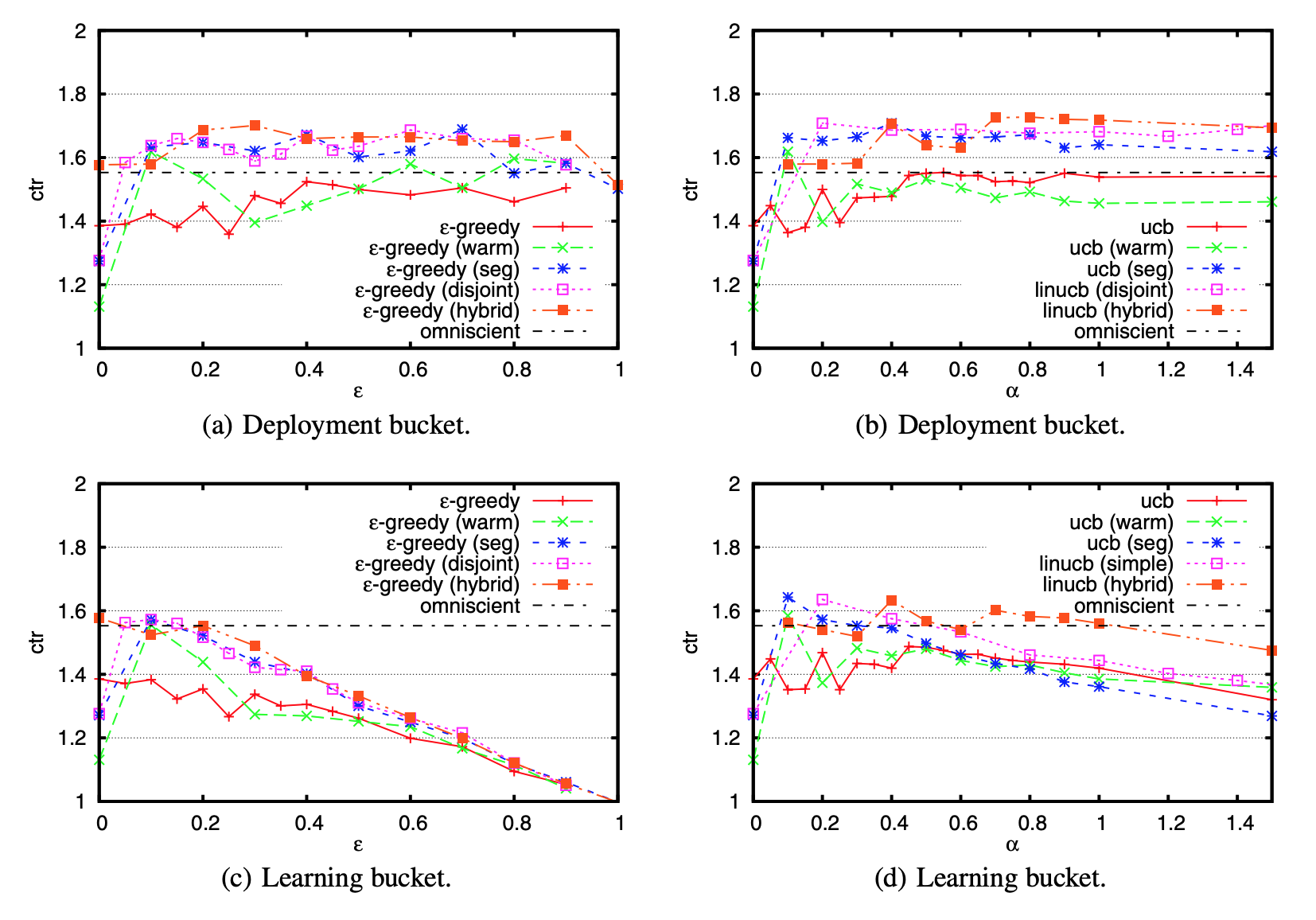그림 2: 파라미터 조정: 조정 데이터셋 1일 치에 대한 모든 알고리즘의 CTR.

우선, 그림 2에서 볼 수 있듯이 학습 버킷 CTR 곡선은 종종 거꾸로 된 U 자형을 그린다. 파라미터(\(\epsilon\) 또는 \(\alpha\))가 너무 작으면 탐색이 불충분하여 알고리즘이 좋은 기사를 식별해내지 못하고 클릭 수가 적다. 반면에 파라미터가 너무 크면 알고리즘이 과도한 탐색을 수행해서 클릭 수를 늘릴 수 있는 기회를 낭비한다. 조정 데이터에 대한 이러한 도표를 기반으로 각 알고리즘마다 적합한 파라미터를 선택하고 다음 이어지는 절에서 평가 데이터로 한 번 더 실험할 것이다.

두 번째로, 변수 없는 버전의 \(\epsilon\)-탐욕과 UCB와 비교하여 웜 스타트 정보가 사용자 관심사와 기사 콘텐츠 간의 더 적합한 대응을 찾는데 크게 도움이 된다는 사실을 도표를 통해 알 수 있다. 특히 \(\epsilon\)-탐욕(웜 스타트)와 ucb(웜 스타트)의 경우 맥락 무관한 정책이 달성 가능한 CTR의 최고값을 갖는 전지적 정책을 능가했다. 그러나 웜 스타트 정보를 사용하는 두 알고리즘의 성능은 온라인으로 가중치를 학습하는 알고리즘만큼 안정적이지 않았다. “웜 스타트”에 대한 오프라인 모형은 무작위 트래픽 전체에 대해 기사 별로 계산된 CTR을 갖고 훈련시켰으므로 \(\epsilon\)-탐욕(웜 스타트)의 경우 \(\epsilon\)이 1에 가까워야 배포 버킷에서 더 안정적인 성능을 얻을 수 있었다. 또한 학습 버킷에서는 사용자가 처음부터 더욱 흥미로워할 기사를 채택하는 식으로 ucb(웜 스타트)가 도움이 됐지만 배포에 가장 적합한 온라인 모형을 결정하는데 ucb(웜 스타트)는 도움이 되지 않았다. ucb는 탐색을 위한 신뢰 구간에 의존하기 때문에 “웜 스타트”를 통해 유입된 초기값 편향을 수정하는 건 어려운 일이다. 대조적으로 모든 온라인 학습 알고리즘이 전지적 정책을 능가했다. 따라서 평가 데이터에 대해서는 웜 스타트 알고리즘을 시행하지 않았다.

세 번째로, \(\epsilon\)-탐욕 알고리즘(그림 2의 왼쪽)은 적절한 파라미터를 사용할 때 배포 버킷에서 UCB(그림 2의 오른쪽)와 비슷한 CTR을 달성한다. 따라서 두 가지 유형의 알고리즘 모두 비슷한 정책을 학습하는 걸로 나타났다. 그러나 실제 버킷 시험에서 진행했던 맥락 무관한 알고리즘의 실험 결과⁸와 일치하게, 학습 버킷의 CTR이 더 낮은 편이다.

마지막으로, 데이터가 희소한 상황에서 알고리즘을 비교하기 위해 30%, 20%, 10%, 5% 그리고 1%가량의 데이터 일부로 각 알고리즘마다 파라미터 조정 절차를 동일하게 반복했다. 알고리즘 3에서 수행한 것처럼 알고리즘의 CTR 평가에는 모든 데이터를 사용했지만 알고리즘 정책 개선에는 사용 가능한 데이터 중 일부만 임의로 선택했다.

5.5.2 검증 데이터를 위한 결과

조정 데이터(그림 2 참조)에 최적화된 파라미터를 사용하여 알고리즘을 평가 데이터에 대해 실행한 후 결과 CTR을 표 1에 요약했다. 또한 이 표는 \(\epsilon\)-탐욕을 기준선 삼아 CTR 상승분을 기재했다. 전지적 정책의 CTR은 1.615이므로 알고리즘 CTR이 이보다 훨씬 높다는 건 개인화에 사용자 / 기사 변수를 효과적으로 사용했음을 의미한다. 표시한 CTR은 무작위 정책의 CTR로 정규화한 것임을 기억하라. 다음 이어지는 절에서 결과를 자세히 살펴보겠다.

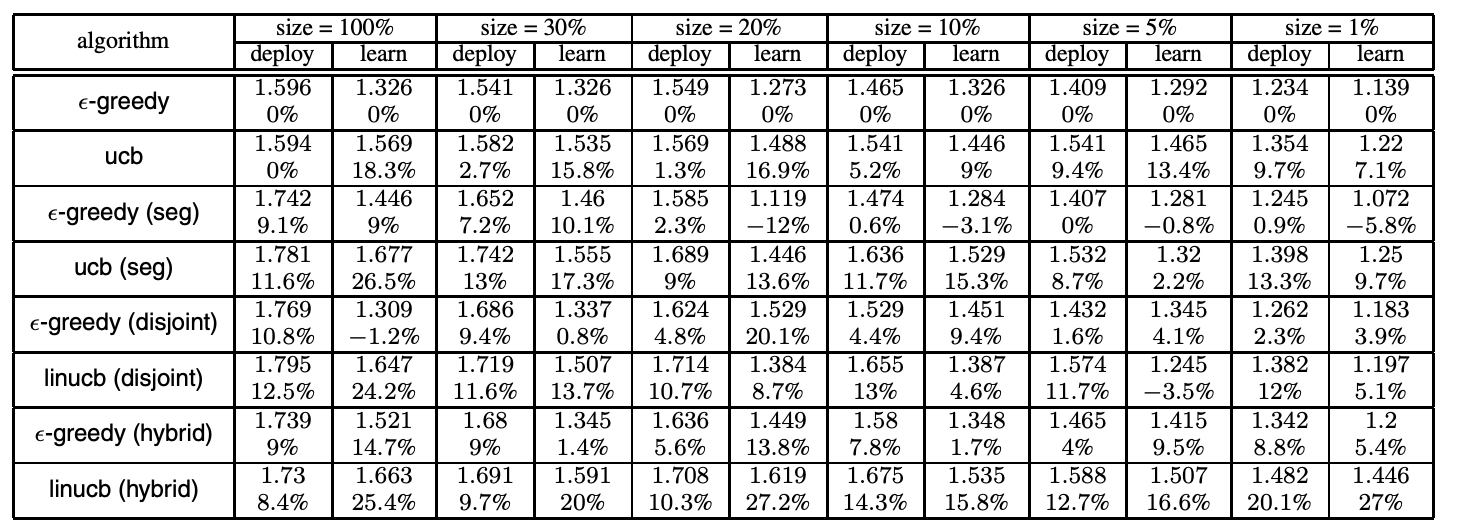표 1: 성능 평가: 배포와 학습 버킷의 1주일치 평가 데이터셋에 대한 모든 알고리즘의 CTR(표에서 각각 “deploy”와 “learn”으로 표시). 백분율이 있는 숫자가 \(\epsilon\)-탐욕과 비교한 CTR 상승분이다.

변수 사용에 대하여

먼저 기사 추천에 변수를 사용하는 것이 도움이 되는지 조사해보자. 사용자 변수를 고려한 \(\epsilon\)-탐욕(세분화/분리/혼합)과 UCB 방법(ucb (세분화)와 linucb(분리/혼합)) 모두 기준선인 \(\epsilon\)-탐욕 대비 결과 CTR을 약 10% 상승시켰다. 이는 표 1에서 확인할 수 있다.
그림 3은 기사 별 CTR(알고리즘이 선택한 경우)이 기본 CTR(맥락 무관한 CTR) 대비 얼마나 향상했는지 보여준다.⁹ 이를 통해 변수 효과를 한눈에 확인할 수 있다. 여기서 기사의 기본 CTR은 임의의 사용자가 해당 기사를 얼마나 관심 있어할지 측정하는 지표로써 이벤트 로그를 통해 추정했다. 따라서 기사의 기본 CTR 대비 결과 CTR의 상승분이 클수록 알고리즘이 관심 있는 사용자에게 해당 기사를 추천했다는 강력한 증거가 된다. 그림 3(a)은 \(\epsilon\)-탐욕이나 ucb가 사용자 정보를 사용하지 않았기 때문에 기사의 CTR을 상승시킬 수 없었음을 보여준다. 대조적으로, 다른 세 도표 모두 개인화 추천을 고려할 때의 이점을 명확히 보여준다. 극단적으로(그림 3(c)) 기사의 CTR 중 하나는 1.31에서 3.03으로 132% 개선되었다.

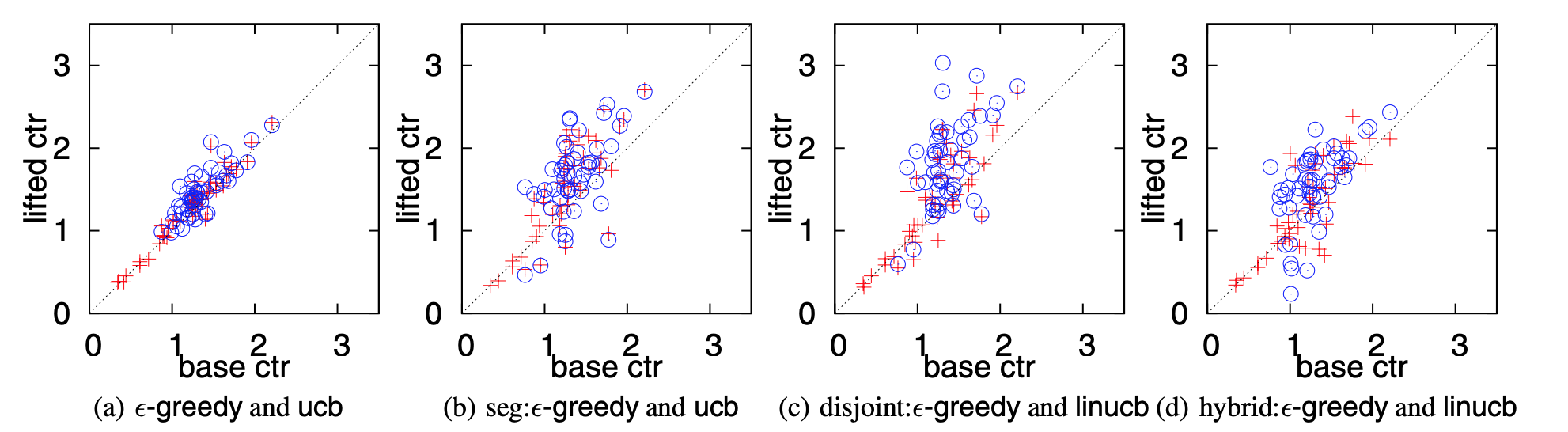그림 3: 평가 데이터를 100% 사용했을 때 가장 많이 선택한 기사 50개에 관한 기본 CTR 대비 결과 CTR(학습 버킷) 상승분의 산점도. 빨간 십자가는 \(\epsilon\)-탐욕 알고리즘을 위한 것이고 파란 원은 UCB 알고리즘을 위한 것이다. 가장 자주 선택한 기사의 집합은 알고리즘마다 다르다. 자세한 내용은 본문을 참조하라.

또한 UCB 방법은 \(\epsilon\)-탐욕 알고리즘과 비교할 때 배포, 학습 버킷 양쪽에서 CTR이 더 높으며 특히 학습 버킷에서 해당 이점이 더욱 크다는 사실에서 조정 데이터의 이전 결과와 일치한다. 2.2절에서 언급한 바와 같이 \(\epsilon\)-탐욕 접근법은 탐색을 위해 기사를 무작위로 선택하기 때문에 유도되는 방향이 없다. 반대로 UCB 방법에서의 탐색은 알고리즘 CTR 추정치에서 불확실성을 측정하는 신뢰 구간에 의해 효과적으로 유도된다. 실험 결과는 UCB 방법의 뛰어난 효용성을 내포하며 다른 많은 응용 분야에서도 비슷한 이점이 있으리라 기대된다.

데이터 크기에 대하여

개인화된 웹 서비스의 난제 중 하나는 응용 프로그램의 규모이다. 예를 들어 본 문제에서 작은 규모의 뉴스 기사 풀은 편집자들이 직접 손으로 선택했다. 그러나 선택 안을 더 많이 가져가고 싶거나 기사 자동 선택 방법을 사용하여 기사 풀을 결정하려는 경우 Yahoo!의 대규모 트래픽을 고려하더라도 기사 개수는 너무 많을 것이다. 따라서 알고리즘은 희소한 데이터에서 사용자 관심사와 기사 콘텐츠 간의 적절한 대응을 신속하게 찾아내는 것이 중요하다. 본 실험에서, 기사 풀을 방대하게 만드는 대신 고정량의 트래픽만 있는 상황을 가정하기 위해 데이터 크기를 인위적으로 (각각 30%, 20%, 10%, 5% 및 1% 수준으로) 줄였다.

비교 결과를 더욱 잘 시각화하기 위해 그림 4의 막대그래프를 사용하여 데이터의 희소성 수준마다 각 알고리즘의 CTR을 그려 넣었다. 몇 가지를 차례로 알 수 있다. 첫째, 데이터의 모든 희소성 수준에서 변수는 여전히 유용했다. 예를 들어 1% 수준에서 ucb(1.354) 대비 linucb(혼합)의 CTR(1.493)은 배포 버킷에서 10.3% 개선되었다.

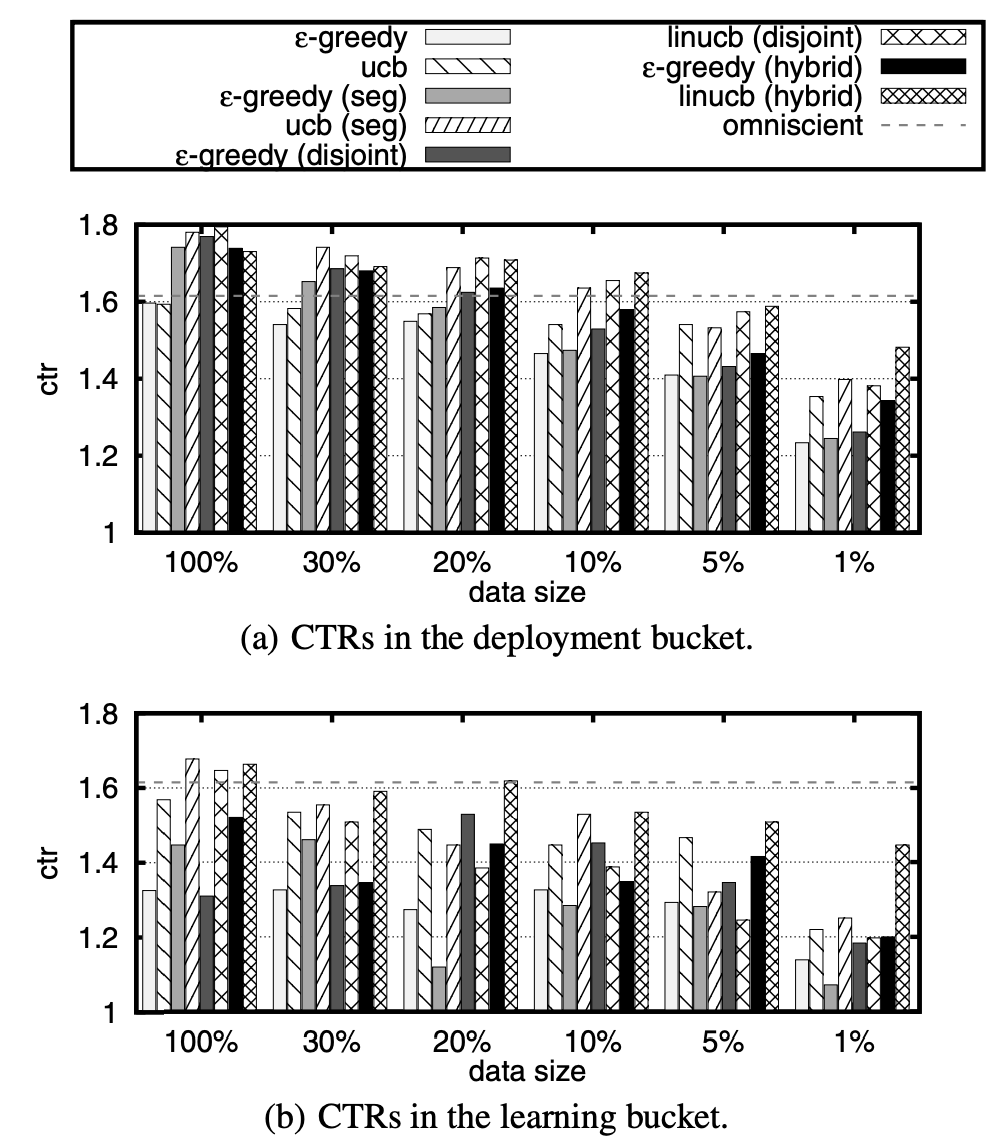그림 4: 다양한 데이터 크기를 가지는 평가 데이터에 대한 CTR.

둘째, UCB 방법은 배포 버킷에서 \(\epsilon\)-탐욕 방법을 지속적으로 능가했다.¹⁰ \(\epsilon\)-탐욕에 대한 이점은 데이터 크기가 작을 때 훨씬 분명했다.

셋째, ucb(세분화)와 linucb(분리)에 비해 linucb(혼합)은 데이터 크기가 작을 때 상당한 이점을 보여주었다. 혼합 모형에서는 모든 기사가 일부 변수를 공유하므로 한 기사의 CTR 정보를 다른 기사에 “전이”시킬 수 있다. 이런 장점은 기사 풀이 클 때 특히 유용하다. 대조적으로 분리 모형의 경우 어떤 기사의 피드백이 다른 기사에게는 딱히 유용하지 않을 것이다. ucb(세분화)도 마찬가지이다. 그림 4(a)는 전이 학습이 데이터가 희소할 때 실제로 도움이 된다는 점을 보여준다.

ucb(세분화)와 linucb(분리)를 비교할 때

그림 4(a)에서 ucb(세분화)와 linucb(분리)의 성능이 비슷한 걸 볼 수 있다. 이는 우연의 일치가 아닐 것이다. 실제로 분리 모형의 변수는 5.2.2절에서 설명한 5개의 군집에 대해 사용자가 속할 수준을 정규화한 숫자임을 기억해라. 따라서 이러한 변수는 ucb(세분화)가 채택한, 사용자 배정 과정의 “연성” 버전으로 볼 수 있다.

그림 5는 가장 가까운 군집, 즉 사용자의 상수가 아닌 변수 5개 중 최대인 구성 요소의 값에 대한 히스토그램이다. 이는 사용자의 집단 소속에 대한 상대적 측정이라고 할 수 있다. 사용자의 대부분은 5개의 군집 중심 중 하나와 매우 근접한 것으로 나타났다. 최대 구성 요소 값에 대해 약 85%의 사용자가 0.5보다 높았으며 그중 약 40%가 0.8보다 높았다. 따라서 해당 변수의 상당수는 두드러진 구성 요소를 갖으므로 변수 벡터는 사용자 집단 배정의 “경성” 버전과 비슷하다.

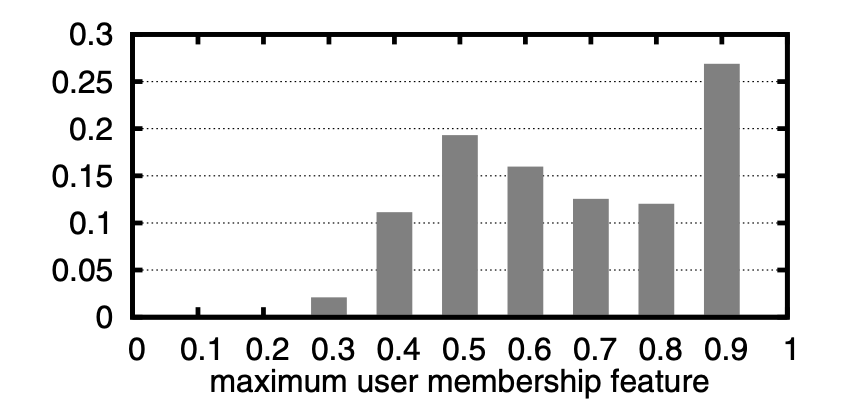그림 5: 사용자의 구성 요소 최댓값에 대한 히스토그램.

linucb(분리)이 ucb(세분화)로부터 변별력을 가지려면 주성분 분석에서 찾은 것 같은 다양한 구성 요소로 변수를 더욱 많이 추가해야 할 것이다.

6. 결론

본 논문은 뉴스 기사 추천 같은 개인화 웹 기반 서비스에 대해 컨텍스츄얼 밴딧 방식으로 접근하였다. 이벤트 로그를 이용하여 밴딧 알고리즘을 직접 평가할 수 있는 간단하고 안정적인 방법론을 제안한 결과 종종 문제가 되는 시뮬레이터 구축 단계를 피할 수 있게 되었다. Yahoo! Front Page 실제 트래픽에 대한 실험을 통해 UCB 방법이 단순하지만 유도되는 방향이 없는 \(\epsilon\)-탐욕 방법보다 성능이 일반적으로 우수하다는 사실을 알게 되었다. 또한 새로운 알고리즘 LinUCB의 경우 데이터가 희소할 때 더 큰 장점을 보여주므로 풀 안의 콘텐츠 개수가 많은 개인화 웹 서비스일수록 더 큰 효용을 가질 수 있다. 앞으로는 온라인 광고와 유사한, 또 다른 종류의 웹 기반 서비스에 사용되는 밴딧 접근 방식을 조사하고 본 논문의 알고리즘을 Banditron 등 연관 방법론과 비교해볼 계획이다. 두 번째 계획은 슬롯 손잡이가 하나의 품목(예컨대 기사)이 아니라 복잡한 오브젝트인 경우도 다룰 수 있게 밴딧 공식과 알고리즘을 확장하는 것이다. 예를 들자면 슬롯 손잡이가 검색된 웹 페이지의 순열에 대응되는 상황, 즉 순위를 매기는 경우이다. 끝으로 사용자의 관심사는 시간에 따라 변하기 때문에 밴딧 알고리즘에서 시간 정보를 고려하는 것도 해봄직하다.