암시적 행렬 분해(고전적인 ALS 방법) 소개와 LightFM을 이용한 순위 학습
by Ethan Rosenthal
Ethan Rosenthal의 Intro to Implicit Matrix Factorization: Classic ALS with Sketchfab Models 외 1편을 번역했습니다.
암시적 행렬 분해 소개: Sketchfab 모델에 적용한 고전적인 ALS 방법
지난 글에서 웹사이트 Sketchfab로부터 암시적 피드백 데이터를 수집하는 방법에 대해 설명했다. 그리고 이 데이터를 사용해 추천 시스템을 실제 구현해보겠다고 이야기했다. 자, 이제 만들어보자!
암시적 피드백을 위한 추천 모형을 살펴보려면 Koren 등이 저술한 논문의 고전 “암시적 피드백 데이터셋을 위한 협업 필터링”(경고: pdf 링크) 중 설명한 모형에서 시작하는 편이 좋겠다. 이 모형은 각종 문헌과 기계학습 라이브러리마다 다양하게 불린다. 여기선 꽤 자주 사용하는 이름 중 하나인 제약적 행렬 가중 분해(WRMF)라고 부르겠다. WRMF는 암시적 행렬 분해에 있어 클래식 록 음악 같은 존재이다. 최신 유행은 아닐지도 몰라도 스타일에서 크게 벗어나지 않는다. 난 이 모형을 사용할 때마다 문제를 잘 해결하고 있다는 확신이 든다. 특히 이 모형은 합리적, 직관적인 의미를 가지고 확장 가능하며 가장 좋은 점은 조정하기 편리하다는 것이다. 확률적 경사 하강 방법의 모형보다 훨씬 적은 수의 하이퍼 파라미터만 갖는다.
명시적 피드백 행렬 분해에 대한 과거 게시물을 떠올려보면 다음과 같은 손실 함수(편향 없는)가 있었다.
\[L_{exp} = \sum_{u, i \in S}(r_{ui} - \mathbf{x}^T_u \cdot \mathbf{y}_i)^2 + \lambda_{x} \sum_u {\lVert \mathbf{x}_u \rVert}^2 + \lambda_{y} \sum_i {\lVert \mathbf{y}_i \rVert}^2\]여기서 \(r_{ui}\)는 사용자-품목 점수 행렬의 요소이고 \(\mathbf{x}_u (\mathbf{y}_i)\)는 사용자 \(u\)(품목 \(i\))의 잠재 요인이며 \(S\)는 사용자-품목 점수의 전체 집합이다.
WRMF는 이 손실 함수를 단순 수정한 것이다.
여기서는 \(S\)의 요소만 합하는 대신 행렬 전체에 대해 합한다. 암시적 피드백이기 때문에 점수가 존재하지 않음을 기억하라. 대신 품목에 대한 사용자의 선호도를 가지고 있다. WRMF 손실 함수에서 점수 행렬 \(r_{ui}\)이 선호도 행렬 \(p_{ui}\)로 바뀌었다. 사용자가 항목과 전혀 상호 작용하지 않았다면 \(p_{ui} = 1\), 그렇지 않으면 \(p_{ui} = 0\)이라고 가정하자.
손실 함수 중 새롭게 나타난 또 다른 항은 \(c_{ui}\)이다. 이를 신뢰도 행렬이라고 부르며 사용자 \(u\)가 품목 \(i\)에 대해 선호도 \(p_{ui}\)를 가짐을 얼마나 신뢰할 수 있는지 대략적으로 설명하는 역할을 한다. 논문에서 저자가 고려하는 신뢰도 공식 중 하나는 상호 작용 횟수에 대한 선형 함수이다. 즉, 사용자가 웹사이트에서 어떤 품목을 클릭한 횟수가 \(d_{ui}\) 라면
\[c_{ui} = 1 + \alpha d_{ui}\]이다. 여기서 \(\alpha\)는 교차검증을 통해 정해지는 하이퍼 파라미터이다. Sketchfab 데이터 사례는 이진 값인 “좋아요”만 있으므로 \(d_{ui} \in 0, 1\)이다.
다시 돌아가면 WRMF는 어떤 품목과 상호 작용한 적 없는 사용자가 해당 품목을 좋아하지 않는다고 가정하진 않는다. WRMF는 해당 사용자가 해당 품목에 대해 부정적인 선호도를 가지고 있다고 가정하지만 신뢰도라는 하이퍼 파라미터를 통해 그 가정을 얼마나 신뢰할지 선택할 수 있다.
자, 이제 예전 명시적 행렬 분해 게시물처럼 이 알고리즘을 최적화하는 방법에 관한 전체적인 전개를 Latex 떡칠로 적어볼 수 있지만 다른 이들이 이미 여러 번 끝내 놨다. 다음은 위대한 StackOverflow의 답변이다. Dirac 표기법으로 전개하는 내용이 마음에 든다면 Sudeep Das 게시물을 확인해라.
WRMF 라이브러리
WRMF를 구현한 오픈 소스 코드는 많은 곳에서 찾을 수 있다. 교차 최소 자승법은 손실 함수를 최적화하는 가장 보편적인 방법이다. 이 방법은 확률적 경사 하강법보다 조정하기가 덜 까다롭고 모형은 처치 곤란 병렬로 돌릴 수 있다.
가장 처음 봤던 해당 알고리즘의 코드는 Chris Johnson 저장소의 것이다. 이 코드는 파이썬으로 작성되었고 희소 행렬을 멋지게 이용하여 일반적인 작업들을 처리한다. Thierry Bertin-Mahieux는 이 코드를 가져와서 파이썬 멀티 프로세싱 라이브러리를 사용하여 병렬 처리했다. 이는 정확도의 손실 없이 상당한 속도 향상을 가져왔다.
Quora의 사람들은 qmf라고 불리는 라이브러리를 가지고 나왔다. 병렬 처리한 qmf는 C++로 짜여있다. 난 사용해보지 않았지만 아마 파이썬 멀티 프로세싱 버전보다 빠를 것이다. 마지막으로 Ben Frederickson은 순수 Cython으로 병렬 코드를 작성해 이곳에 올려놓았다. 이건 성능적인 측면에서 다른 파이썬 버전들을 납작하게 눌러버렸고 심지어 qmf보다 다소 빠르다(좀 이상하지만).
나는 이 게시물을 위해 Ben의 라이브러리를 사용하기로 했다. 왜냐면 (1) 파이썬으로 계속 개발할 수 있고 (2) 매우 빠르기 때문이다. 라이브러리를 포크한 뒤 격자 탐색과 학습 곡선 계산을 손쉽게 수행하기 위해 알고리즘을 감싸는 조그만 클래스를 작성했다. 어떤 테스트도 해보지 않아 사용자가 위험을 직접 감수해야겠지만 여기 내 포크를 자유롭게 체크 아웃해서 써도 된다. :)
데이터 주무르기
여기까지 하고 WRMF 모형을 훈련시켜서 Sketchfab 모델을 추천해보자!
첫 번째 단계는 데이터를 불러와서 “사용자 수” 곱하기 “품목 수” 크기의 상호 작용 행렬로 변환하는 것이다. 데이터의 각 행은 사용자가 Sketchfab 웹사이트에서 “좋아요”를 누른 모델을 나타내며 현재 csv 형태로 저장되었다. 첫 번째 열은 모델 이름이고 두 번째 열은 고유한 모델 ID(mid)이며 세 번째 열은 익명화된 사용자 ID(uid)이다.
%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import scipy.sparse as sparse
import pickle
import csv
import implicit
import itertools
import copy
plt.style.use('ggplot')
df = pd.read_csv('../data/model_likes_anon.psv',
sep='|', quoting=csv.QUOTE_MINIMAL,
quotechar='\\')
df.head()
| modelname | mid | uid | |
|---|---|---|---|
| 0 | 3D fanart Noel From Sora no Method | 5dcebcfaedbd4e7b8a27bd1ae55f1ac3 | 7ac1b40648fff523d7220a5d07b04d9b |
| 1 | 3D fanart Noel From Sora no Method | 5dcebcfaedbd4e7b8a27bd1ae55f1ac3 | 2b4ad286afe3369d39f1bb7aa2528bc7 |
| 2 | 3D fanart Noel From Sora no Method | 5dcebcfaedbd4e7b8a27bd1ae55f1ac3 | 1bf0993ebab175a896ac8003bed91b4b |
| 3 | 3D fanart Noel From Sora no Method | 5dcebcfaedbd4e7b8a27bd1ae55f1ac3 | 6484211de8b9a023a7d9ab1641d22e7c |
| 4 | 3D fanart Noel From Sora no Method | 5dcebcfaedbd4e7b8a27bd1ae55f1ac3 | 1109ee298494fbd192e27878432c718a |
print('중복 행 수: ' + str(df.duplicated().sum()))
print('이상하네 - 그냥 버리자')
df.drop_duplicates(inplace=True)
중복 행 수 155
이상하네 - 그냥 버리자
df = df[['uid', 'mid']]
df.head()
| uid | mid | |
|---|---|---|
| 0 | 7ac1b40648fff523d7220a5d07b04d9b | 5dcebcfaedbd4e7b8a27bd1ae55f1ac3 |
| 1 | 2b4ad286afe3369d39f1bb7aa2528bc7 | 5dcebcfaedbd4e7b8a27bd1ae55f1ac3 |
| 2 | 1bf0993ebab175a896ac8003bed91b4b | 5dcebcfaedbd4e7b8a27bd1ae55f1ac3 |
| 3 | 6484211de8b9a023a7d9ab1641d22e7c | 5dcebcfaedbd4e7b8a27bd1ae55f1ac3 |
| 4 | 1109ee298494fbd192e27878432c718a | 5dcebcfaedbd4e7b8a27bd1ae55f1ac3 |
n_users = df.uid.unique().shape[0]
n_items = df.mid.unique().shape[0]
print('사용자 수: {}'.format(n_users))
print('모델 개수: {}'.format(n_items))
print('희소 정도: {:4.3f}%'.format(float(df.shape[0]) / float(n_users*n_items) * 100))
사용자 수: 62583
모델 개수: 28806
희소 정도: 0.035%
암시적 피드백 데이터가 희소해도 추천 성능은 괜찮게 나올 테지만 상호작용 행렬을 밀집되게 만들면 더 좋아질 수 있다. 좋아요가 최소 5번 이상 있는 모델만 데이터를 수집했다. 그러나 사용자 전부가 좋아요를 최소 5번 이상 누른 건 아닐 수 있다. 좋아요를 누른 모델이 5개 미만인 사용자를 날려버리자. 해당 사용자를 날려버리면서 일부 모델이 좋아요 5개 미만으로 다시 떨어질 수 있다. 수렴할 때까지 사용자와 모델 날리는 작업을 교대로 반복하자.
def threshold_likes(df, uid_min, mid_min):
n_users = df.uid.unique().shape[0]
n_items = df.mid.unique().shape[0]
sparsity = float(df.shape[0]) / float(n_users*n_items) * 100
print('최초 좋아요 정보')
print('사용자 수: {}'.format(n_users))
print('모델 개수: {}'.format(n_items))
print('희소 정도: {:4.3f}%'.format(sparsity))
done = False
while not done:
starting_shape = df.shape[0]
mid_counts = df.groupby('uid').mid.count()
df = df[~df.uid.isin(mid_counts[mid_counts < mid_min].index.tolist())]
uid_counts = df.groupby('mid').uid.count()
df = df[~df.mid.isin(uid_counts[uid_counts < uid_min].index.tolist())]
ending_shape = df.shape[0]
if starting_shape == ending_shape:
done = True
assert(df.groupby('uid').mid.count().min() >= mid_min)
assert(df.groupby('mid').uid.count().min() >= uid_min)
n_users = df.uid.unique().shape[0]
n_items = df.mid.unique().shape[0]
sparsity = float(df.shape[0]) / float(n_users*n_items) * 100
print('최종 좋아요 정보')
print('사용자 수: {}'.format(n_users))
print('모델 개수: {}'.format(n_items))
print('희소 정도: {:4.3f}%'.format(sparsity))
return df
df_lim = threshold_likes(df, 5, 5)
최초 좋아요 정보
사용자 수: 62583
모델 개수: 28806
희소 정도: 0.035%
최종 좋아요 정보
사용자 수: 15274
모델 개수: 25655
희소 정도: 0.140%
좋다, 희소 정도가 0.1% 이상이므로 괜찮은 추천을 하기에 적당하다. 이제 상호작용 또는 “좋아요” 행렬을 위해 각각의 uid와 mid를 상응하는 행과 열로 매핑해야 한다. 이 작업은 파이썬 딕셔너리로 간단하게 할 수 있다.
# 매핑 만들기
mid_to_idx = {}
idx_to_mid = {}
for (idx, mid) in enumerate(df_lim.mid.unique().tolist()):
mid_to_idx[mid] = idx
idx_to_mid[idx] = mid
uid_to_idx = {}
idx_to_uid = {}
for (idx, uid) in enumerate(df_lim.uid.unique().tolist()):
uid_to_idx[uid] = idx
idx_to_uid[idx] = uid
마지막 단계는 실제로 행렬을 만드는 작업이다. 메모리를 너무 많이 차지하지 않도록 희소 행렬을 사용한다. 희소 행렬은 여러 형태로 제공되기 때문에 좀 까다롭다. 그리고 이들 간에 성능 상 어마어마한 트레이드오프가 있다. 아래는 좋아요 행렬을 구축하는 아주 느린 방법이다. %%timeit을 돌렸지만 실행 완료를 기다리자니 지루해졌다.
# # 이건 실행하지 말자!
# num_users = df_lim.uid.unique().shape[0]
# num_items = df_lim.mid.unique().shape[0]
# likes = sparse.csr_matrix((num_users, num_items), dtype=np.float64)
# for row in df_lim.itertuples():
# likes[uid_to_idx[uid], mid_to_idx[row.mid]] = 1.0
그 대신 아래 것은 50만 명의 행렬을 만들고 있다고 생각하면 꽤 빠르다.
def map_ids(row, mapper):
return mapper[row]
%%timeit
I = df_lim.uid.apply(map_ids, args=[uid_to_idx]).as_matrix()
J = df_lim.mid.apply(map_ids, args=[mid_to_idx]).as_matrix()
V = np.ones(I.shape[0])
likes = sparse.coo_matrix((V, (I, J)), dtype=np.float64)
likes = likes.tocsr()
1 loop, best of 3: 876 ms per loop
I = df_lim.uid.apply(map_ids, args=[uid_to_idx]).as_matrix()
J = df_lim.mid.apply(map_ids, args=[mid_to_idx]).as_matrix()
V = np.ones(I.shape[0])
likes = sparse.coo_matrix((V, (I, J)), dtype=np.float64)
likes = likes.tocsr()
교차 검증: 데이터 분할
자, 좋아요 행렬을 훈련과 시험 행렬로 분할할 필요가 있다. 이를 다소 교묘하게(이렇게 한 단어로 끝낼 문제일까?) 진행했다. 최적화 측정 단위로 precision@k를 이용할 생각이다. k는 5 정도가 좋을 것 같다. 그러나 일부 사용자의 경우 훈련에서 시험 쪽으로 5개 품목을 이동시키면 훈련 셋에 데이터가 남아 있지 않을 수 있다(사람마다 좋아요가 최소 5개임을 기억하자). 따라서 train_test_split은 데이터 일부를 시험 셋으로 이동시키기 전에 좋아요가 적어도 2*k(이 경우 10개) 이상인 사람들을 찾는다. 교차 검증은 좋아요가 많은 사용자 쪽으로 편향될 것이 분명하다. 그래도 가보자.
def train_test_split(ratings, split_count, fraction=None):
"""
추천 데이터를 훈련 셋과 시험 셋으로 분할하기
매개변수
------
ratings: scipy.sparse 행렬
사용자와 품목 간의 상호작용.
split_count: 정수
훈련 셋에서 시험 셋으로 이동시킬 사용자 당 사용자-품목-상호작용 개수.
fractions: 부동소수점
상호작용 일부를 시험 셋으로 분할시킬 사용자 비율. 만약 None이면 사용자 전체를 고려한다.
"""
# 참고: 아래 작업을 하기 위한 가장 빠른 방법은 아닐 것이다.
train = ratings.copy().tocoo()
test = sparse.lil_matrix(train.shape)
if fraction:
try:
user_index = np.random.choice(
np.where(np.bincount(train.row) >= split_count * 2)[0],
replace=False,
size=np.int32(np.floor(fraction * train.shape[0]))
).tolist()
except:
print(('상호작용 개수가 {} 넘는 사용자로'
'{} 비율 채우기 어려움')\
.format(2*k, fraction))
raise
else:
user_index = range(train.shape[0])
train = train.tolil()
for user in user_index:
test_ratings = np.random.choice(ratings.getrow(user).indices,
size=split_count,
replace=False)
train[user, test_ratings] = 0.
# 점수의 경우 지금은 단지 1.0이다.
test[user, test_ratings] = ratings[user, test_ratings]
# 시험 셋과 훈련 셋은 절대 겹치지 말아야 한다.
assert(train.multiply(test).nnz == 0)
return train.tocsr(), test.tocsr(), user_index
train, test, user_index = train_test_split(likes, 5, fraction=0.2)
교차 검증: 격자 탐색
이제 데이터가 훈련과 시험 행렬로 분할되었으므로 거대한 격자 탐색을 실행하여 하이퍼 파라미터를 최적화하자. 최적화시킬 파라미터는 4개 있다.
1.num_factors: 잠재적 요인의 개수 또는 모형이 갖는 차원의 정도.
2.regularization: 사용자와 품목 요인에 대한 정규화 척도.
3.alpha: 신뢰도 척도 항목.
4.iterations: 교대 최소 자승법를 통한 최적화 수행 시 반복 횟수.
평균 제곱 오차(MSE)와 k까지의 정밀도(p@k)를 따라가며 확인할 생각이지만 둘 중 후자에 주로 신경을 쓸 것이다. 측정 단위 계산을 돕고 훈련 로그를 멋지게 출력하기 위해 몇 가지 함수를 아래에 작성했다. 여러 다른 하이퍼 파라미터 조합에 대해 일련의 학습 곡선(즉, 훈련 과정의 각 단계마다 성능 측정 단위를 평가)을 계산할 것이다. scikit-learn에 감사한다. 오픈소스이기에 기본적으로 GridSearchCV 코드를 베껴서 만들었다.
from sklearn.metrics import mean_squared_error
def calculate_mse(model, ratings, user_index=None):
preds = model.predict_for_customers()
if user_index:
return mean_squared_error(ratings[user_index, :].toarray().ravel(),
preds[user_index, :].ravel())
return mean_squared_error(ratings.toarray().ravel(),
preds.ravel())
def precision_at_k(model, ratings, k=5, user_index=None):
if not user_index:
user_index = range(ratings.shape[0])
ratings = ratings.tocsr()
precisions = []
# 참고: 아래 코드는 대량의 데이터셋인 경우 실행이 불가능할 수 있다.
predictions = model.predict_for_customers()
for user in user_index:
# 대량의 데이터셋인 경우 아래와 같이 예측을 행 단위로 계산해라.
# predictions = np.array([model.predict(row, i) for i in xrange(ratings.shape[1])])
top_k = np.argsort(-predictions[user, :])[:k]
labels = ratings.getrow(user).indices
precision = float(len(set(top_k) & set(labels))) / float(k)
precisions.append(precision)
return np.mean(precisions)
def print_log(row, header=False, spacing=12):
top = ''
middle = ''
bottom = ''
for r in row:
top += '+{}'.format('-'*spacing)
if isinstance(r, str):
middle += '| {0:^{1}} '.format(r, spacing-2)
elif isinstance(r, int):
middle += '| {0:^{1}} '.format(r, spacing-2)
elif isinstance(r, float):
middle += '| {0:^{1}.5f} '.format(r, spacing-2)
bottom += '+{}'.format('='*spacing)
top += '+'
middle += '|'
bottom += '+'
if header:
print(top)
print(middle)
print(bottom)
else:
print(middle)
print(top)
def learning_curve(model, train, test, epochs, k=5, user_index=None):
if not user_index:
user_index = range(train.shape[0])
prev_epoch = 0
train_precision = []
train_mse = []
test_precision = []
test_mse = []
headers = ['epochs', 'p@k train', 'p@k test',
'mse train', 'mse test']
print_log(headers, header=True)
for epoch in epochs:
model.iterations = epoch - prev_epoch
if not hasattr(model, 'user_vectors'):
model.fit(train)
else:
model.fit_partial(train)
train_mse.append(calculate_mse(model, train, user_index))
train_precision.append(precision_at_k(model, train, k, user_index))
test_mse.append(calculate_mse(model, test, user_index))
test_precision.append(precision_at_k(model, test, k, user_index))
row = [epoch, train_precision[-1], test_precision[-1],
train_mse[-1], test_mse[-1]]
print_log(row)
prev_epoch = epoch
return model, train_precision, train_mse, test_precision, test_mse
def grid_search_learning_curve(base_model, train, test, param_grid,
user_index=None, patk=5, epochs=range(2, 40, 2)):
"""
sklearn 격자 탐색을 보고 "영감을 얻었음"(훔쳤음)
https://github.com/scikit-learn/scikit-learn/blob/master/sklearn/model_selection/_search.py
"""
curves = []
keys, values = zip(*param_grid.items())
for v in itertools.product(*values):
params = dict(zip(keys, v))
this_model = copy.deepcopy(base_model)
print_line = []
for k, v in params.items():
setattr(this_model, k, v)
print_line.append((k, v))
print(' | '.join('{}: {}'.format(k, v) for (k, v) in print_line))
_, train_patk, train_mse, test_patk, test_mse = learning_curve(this_model, train, test,
epochs, k=patk, user_index=user_index)
curves.append({'params': params,
'patk': {'train': train_patk, 'test': test_patk},
'mse': {'train': train_mse, 'test': test_mse}})
return curves
아래 파라미터 격자가 엄청 거대하기 때문에 6년 된 4-코어 i5로 돌리는데 2일이나 걸렸다. 성능 측정 함수가 실제 훈련 과정보다 조금 더 느린 것으로 나타났다. 이 함수들은 간단히 병렬화할 수 있으며 나중에 작업해 볼 생각이다.
param_grid = {'num_factors': [10, 20, 40, 80, 120],
'regularization': [0.0, 1e-5, 1e-3, 1e-1, 1e1, 1e2],
'alpha': [1, 10, 50, 100, 500, 1000]}
base_model = implicit.ALS()
curves = grid_search_learning_curve(base_model, train, test,
param_grid,
user_index=user_index,
patk=5)
훈련 로그는 말도 안 되게 길긴 한데 여기를 클릭해서 확인할 수 있다. 다음은 최고 결과를 수행한 출력이다.
alpha: 50 | num_factors: 40 | regularization: 0.1
+------------+------------+------------+------------+------------+
| epochs | p@k train | p@k test | mse train | mse test |
+============+============+============+============+============+
| 2 | 0.33988 | 0.02541 | 0.01333 | 0.01403 |
+------------+------------+------------+------------+------------+
| 4 | 0.31395 | 0.03916 | 0.01296 | 0.01377 |
+------------+------------+------------+------------+------------+
| 6 | 0.30085 | 0.04231 | 0.01288 | 0.01372 |
+------------+------------+------------+------------+------------+
| 8 | 0.29175 | 0.04231 | 0.01285 | 0.01370 |
+------------+------------+------------+------------+------------+
| 10 | 0.28638 | 0.04407 | 0.01284 | 0.01370 |
+------------+------------+------------+------------+------------+
| 12 | 0.28684 | 0.04492 | 0.01284 | 0.01371 |
+------------+------------+------------+------------+------------+
| 14 | 0.28533 | 0.04571 | 0.01285 | 0.01371 |
+------------+------------+------------+------------+------------+
| 16 | 0.28389 | 0.04689 | 0.01285 | 0.01372 |
+------------+------------+------------+------------+------------+
| 18 | 0.28454 | 0.04695 | 0.01286 | 0.01373 |
+------------+------------+------------+------------+------------+
| 20 | 0.28454 | 0.04728 | 0.01287 | 0.01374 |
+------------+------------+------------+------------+------------+
| 22 | 0.28409 | 0.04761 | 0.01288 | 0.01376 |
+------------+------------+------------+------------+------------+
| 24 | 0.28251 | 0.04689 | 0.01289 | 0.01377 |
+------------+------------+------------+------------+------------+
| 26 | 0.28186 | 0.04656 | 0.01290 | 0.01378 |
+------------+------------+------------+------------+------------+
| 28 | 0.28199 | 0.04676 | 0.01291 | 0.01379 |
+------------+------------+------------+------------+------------+
| 30 | 0.28127 | 0.04669 | 0.01292 | 0.01380 |
+------------+------------+------------+------------+------------+
| 32 | 0.28173 | 0.04650 | 0.01292 | 0.01381 |
+------------+------------+------------+------------+------------+
| 34 | 0.28153 | 0.04650 | 0.01293 | 0.01382 |
+------------+------------+------------+------------+------------+
| 36 | 0.28166 | 0.04604 | 0.01294 | 0.01382 |
+------------+------------+------------+------------+------------+
| 38 | 0.28153 | 0.04637 | 0.01295 | 0.01383 |
+------------+------------+------------+------------+------------+
최고 결과 수행 시 학습 곡선이 어떻게 생겼는지 살펴보도록 하자.
best_curves = sorted(curves, key=lambda x: max(x['patk']['test']), reverse=True)
print(best_curves[0]['params'])
max_score = max(best_curves[0]['patk']['test'])
print(max_score)
iterations = range(2, 40, 2)[best_curves[0]['patk']['test'].index(max_score)]
print('Epoch: {}'.format(iterations))
print(best_curves[0]['params'])
max_score = max(best_curves[0]['patk']['test'])
print(max_score)
iterations = range(2, 40, 2)[best_curves[0]['patk']['test'].index(max_score)]
print('Epoch: {}'.format(iterations))
{'alpha': 50, 'num_factors': 40, 'regularization': 0.1}
0.0476096922069
Epoch: 22
import seaborn as sns
sns.set_style('white')
fig, ax = plt.subplots()
sns.despine(fig);
plt.plot(epochs, best_curves[0]['patk']['test']);
plt.xlabel('Epochs', fontsize=24);
plt.ylabel('Test p@k', fontsize=24);
plt.xticks(fontsize=18);
plt.yticks(fontsize=18);
plt.title('Best learning curve', fontsize=30);
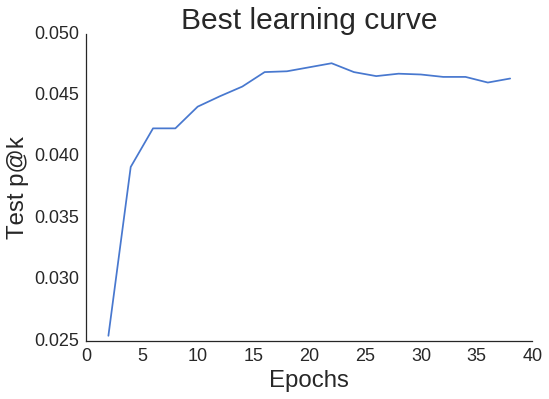
곡선이 약간 들쭉날쭉하지만 최고 에폭인 22를 지나면 곡선이 유의하게 감소하지 않는다. 즉, 조기 종료 사용에 너무 조심스럽지 않아도 된다(p@k가 신경 써야 할 유일한 측정 단위라면).
모든 학습 곡선을 그려볼 수 있으며 하이퍼 파라미터의 차이가 확연한 성능의 차이를 가져옴을 알 수 있다.
all_test_patks = [x['patk']['test'] for x in best_curves]
fig, ax = plt.subplots(figsize=(8, 10));
sns.despine(fig);
epochs = range(2, 40, 2)
totes = len(all_test_patks)
for i, test_patk in enumerate(all_test_patks):
ax.plot(epochs, test_patk,
alpha=1/(.1*i+1),
c=sns.color_palette()[0]);
plt.xlabel('Epochs', fontsize=24);
plt.ylabel('Test p@k', fontsize=24);
plt.xticks(fontsize=18);
plt.yticks(fontsize=18);
plt.title('Grid-search p@k traces', fontsize=30);
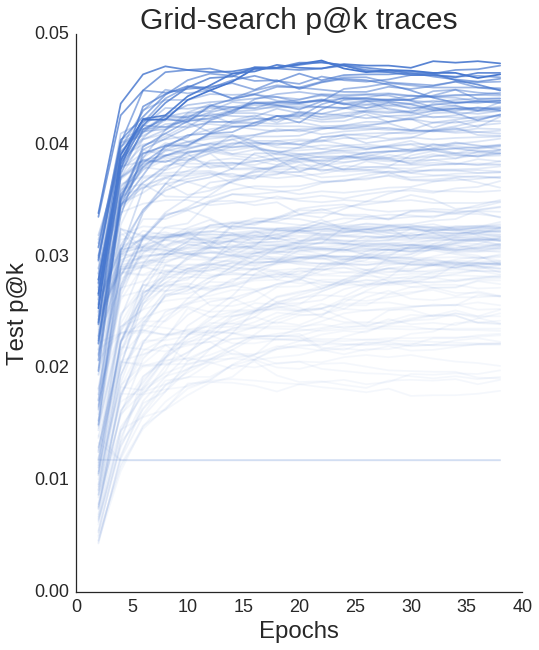
스케치 추천하기
모든 과정 끝에 최적 하이퍼 파라미터를 마침내 얻었다. 이제 더욱 세밀한 격자 탐색을 수행하거나 사용자와 품목 정규화 효과의 비율을 변화시킴에 따라 바뀌는 결과를 살펴볼 수 있다. 그러나 2일을 또 기다리고 싶지는 않았다…
최적 하이퍼 파라미터를 사용하여 모든 데이터로 WRMF 모형을 훈련시키고 품목 대 품목 추천을 시각화해보자. 사용자 대 사용자 추천은 시각화하거나 얼마나 정확한지 감을 잡기 다소 어렵다.
params = best_curves[0]['params']
params['iterations'] = range(2, 40, 2)[best_curves[0]['patk']['test'].index(max_score)]
bestALS = implicit.ALS(**params)
bestALS.fit(likes)
품목 대 품목 추천을 얻기 위해 ALS 클래스에 predict_for_items라는 작은 메서드를 만들었다. 이건 본질적으로 품목 벡터 모든 조합 간의 내적이다. norm=True(기본값)로 하면 이 내적은 각 품목 벡터의 길이로 정규화되어 코사인 유사도와 같게 된다. 이는 유사한 두 품목이 내재 또는 잠재 공간 안에서 얼마나 유사한지 알려준다.
def predict_for_items(self, norm=True):
"""모든 품목에 대한 품목 추천"""
pred = self.item_vectors.dot(self.item_vectors.T)
if norm:
norms = np.array([np.sqrt(np.diagonal(pred))])
pred = pred / norms / norms.T
return pred
item_similarities = bestALS.predict_for_items()
이제 일부 모델들과 그와 연관된 추천들을 시각화해서 추천 모형이 얼마나 잘 동작하는지 느껴보도록 하자. 모델의 섬네일을 가져오기 위해 Sketchfab API에 간단히 질의하면 된다. 아래는 품목 유사도, 색인 그리고 색인-mid 매퍼를 사용하여 추천의 섬네일 URL 목록을 반환하는 도우미 함수이다. 첫 번째 추천은 코사인 유사도가 1인 관계로 항상 본 모델 자신임을 유의하라.
import requests
def get_thumbnails(sim, idx, idx_to_mid, N=10):
row = sim[idx, :]
thumbs = []
for x in np.argsort(-row)[:N]:
response = requests.get('https://sketchfab.com/i/models/{}'.format(idx_to_mid[x])).json()
thumb = [x['url'] for x in response['thumbnails']['images'] if x['width'] == 200 and x['height']==200]
if not thumb:
print('no thumbnail')
else:
thumb = thumb[0]
thumbs.append(thumb)
return thumbs
thumbs = get_thumbnails(item_similarities, 0, idx_to_mid)
print(thumbs[0])
https://dg5bepmjyhz9h.cloudfront.net/urls/5dcebcfaedbd4e7b8a27bd1ae55f1ac3/dist/thumbnails/a59f9de0148e4986a181483f47826fe0/200x200.jpeg
이제 HTML 및 핵심 IPython 기능을 사용하여 이미지를 표시할 수 있다.
from IPython.display import display, HTML
def display_thumbs(thumbs, N=5):
thumb_html = "<img style='width: 160px; margin: 0px; \
border: 1px solid black;' src='{}' />"
images = ''
display(HTML('<font size=5>'+'Input Model'+'</font>'))
display(HTML(thumb_html.format(thumbs[0])))
display(HTML('<font size=5>'+'Similar Models'+'</font>'))
for url in thumbs[1:N+1]:
images += thumb_html.format(url)
display(HTML(images))
# 색인 임의로 고르기
rand_model = np.random.randint(0, len(idx_to_mid))
display_thumbs(get_thumbnails(item_similarities, rand_model, idx_to_mid))
입력 모델

유사 모델

# 또 다른 색인 임의로 고르기
rand_model = np.random.randint(0, len(idx_to_mid))
display_thumbs(get_thumbnails(item_similarities, rand_model, idx_to_mid))
입력 모델

유사 모델

# 행운을 빌며 하나 더
rand_model = np.random.randint(0, len(idx_to_mid))
display_thumbs(get_thumbnails(item_similarities, rand_model, idx_to_mid))
입력 모델
유사 모델

추천이 완벽하진 않지만(위의 경찰차+녹색 괴물 참조) 추천 모형이 유사도를 학습한 건 분명해 보인다.
한 걸음 물러서서 잠시 생각해보자.
알고리즘은 이 모델들이 어떤 모습인지, 어떤 태그가 붙어있는지, 또는 그린 이가 누구인지 아무것도 모른다. 알고리즘은 단지 어떤 사용자가 어떤 모델을 좋아했는지 알 뿐이다. 이런 점을 생각하면 꽤 놀랍다.
그다음은?
오늘은 암시적 MF계의 클래식 록 음악인 제약적 행렬 가중 분해를 배웠다. 다음번에는 순위 학습이라고 암시적 피드백 모형을 최적화하는 또 다른 방법에 대해 알아볼 것이다. 순위 학습 모형을 사용하면 모델과 사용자에 대한 추가 정보(예: 모델에 할당한 카테고리 및 태그)를 포함시킬 수 있다. 그 후에 이미지와 사전 학습한 신경망을 적용한 비지도 추천을 이러한 방법과 어떻게 비교할 수 있는지 살펴보고 마지막으로 이 추천들을 최종 사용자에게 제공할 플라스크 앱을 제작할 것이다.
계속 지켜봐 주길!
LightFM을 이용한 Sketchfab 모델 순위 학습
암시적 행렬 분해를 소개하는 마지막 글이며 재미있는 것들을 다룰 것이다. 암시적 행렬 분해를 위한 또 다른 방법, 순위 학습을 살펴본 다음 라이브러리 LightFM을 사용하여 부가 정보를 추천 모형에 녹일 것이다. 다음으로 하이퍼 파라미터 교차 검증을 scikit-optimize를 이용하여 격자 탐색보다 더 똑똑하게 해낼 것이다. 마지막으로 사용자 및 품목과 동일한 공간에 부가 정보를 임베드시켜 사용자 대 품목 그리고 품목 대 품목의 단순 추천을 넘어설 것이다. 가자!
과거로부터의 교훈
Birchbox에서 일하기 시작했을 때 암시적 피드백 행렬 분해 추천 시스템에 사용자의 풍부한 정보를 녹여낼 수 있는 방법을 모색해야만 했다. 내가 뭘 하고 있는 건지 전혀 감이 안 왔다. 구글 검색을 많이 해봤다. 추천 시스템에는 크게 두 가지 패러다임, 즉 사용자의 인구 통계학적 데이터가 있고 다른 유사 사용자를 찾기 위해 해당 데이터를 사용하는 내용 기반의 접근법 그리고 각 사용자가 상호작용 품목을 평가한 내용이 데이터로 있는 “점수 기반” 접근법이 따로 있어서 이는 어려운 문제였다. 나는 두 접근 방식이 결합되길 원했다.
조사 자료를 읽다 보니 고전, 추천 시스템을 위한 행렬 분해 기법(pdf 링크) 내용 중에 “부가적 입력 원천” 절이 있었다. 여기에는 소위 “부가 정보”를 추천 시스템에 녹이는 접근법이 나와있다. 아이디어는 상대적으로 단순하다.(행렬 분해로 인해 머리를 부여잡게 만드는 초기 장벽에 비하면 단순하다.) 정규 행렬 분해 모형에서 사용자 \(u\)는 사용자의 잠재 요인(이에 대한 배경 설명은 이전 게시물들을 봐라)을 담고 있는 단일 벡터 \(\mathbf{x}_u\)로 표현된다. 자, 해당 사용자에 대한 인구 통계학적 정보가 다음과 같이 있다.
| 변수 | 값 |
|---|---|
| 성별 | 여성 |
| 연령대 | 25-34 |
| 소득 구간 | $65-79K |
이 변수들 각각을 “속성-공간” \(A\)로 원-핫-인코딩할 수 있고 각각의 속성 \(a\)가 잠재 벡터 \(\mathbf{s}_a\)를 갖는다고 가정하자. 마지막으로 “총” 사용자 벡터는 원래 사용자 벡터 \(\mathbf{x}_u\)에 연관된 속성 벡터들을 더한 것이라고 가정하자. 만약 \(N(u)\)가 사용자 \(u\)에 속하는 속성 집합을 나타낸다면 총 사용자 벡터는 아래와 같다.
\[\mathbf{x}_u + \sum_{a \in N(u)} \mathbf{s}_a\]품목의 부가 정보에 대한 가정으로 동일한 집합을 만들 수 있다. 이제 추천을 통해 더 나은 결과를 얻을 수 있을뿐더러 벡터를, 그리고 결과적으로 부가 정보 벡터 간의 유사도를 학습할 수 있다. 이에 대한 일반적인 개요는 Dia & Co의 기술 블로그에 쓴 게시물을 참조하라.
좋다, 접근법은 명확하다. 아마도 마지막 게시물의 암시적 피드백 목적 함수에 이것을 더하고 해를 구할 것이다. 맞을까? 글쎄, 수리적으로 풀어봤지만 불행히도 이건 기존 방식을 확장하여 풀 수 없었다. 부가 정보 벡터에 대한 집합을 사용하면 마지막 게시물의 교대 최소 자승법(ALS)이 3방향의 교대 문제가 된다. ALS 최적화의 경우 데이터 희소성을 이용하여 계산의 크기를 바꾸는 묘수가 있다. 그러나 이 묘수를 ALS 단계에서 부가 정보 벡터의 해를 구할 경우 사용할 수 없다.
이제 어떻게 해야 할까?
순위 학습 - BPR
마지막 게시물의 목적 함수에 대해 ALS나 흔히 쓰는 확률적 경사하강법(SGD)이 아닌, 암시적 피드백 행렬 분해 문제를 최적화하는 또 다른 해법이 있다. 이 최적화 방법은 보통 순위 학습이라는 이름으로 알려졌고 정보 검색 이론에서 연구가 시작됐다.
암시적 피드백에 대해 순위를 학습하기 위한 고전적 방법은 논문 BPR: 베이즈 개인화 순위 매기기(pdf 링크)에 나와있다. 암시적 피드백과 행렬 분해 모든 면에서 업적이 대단한 Steffen Rendle이 이 논문의 주저자이다. 긍정적 품목과 부정적 품목에 대해 각각 표본 추출하고 쌍 별로 비교를 수행하는 것이 핵심 아이디어이다. 이 예에서 데이터셋은 사용자가 웹사이트에서 다양한 품목을 클릭한 횟수로 구성된다. BPR은 (단순화된 형태로는) 다음과 같이 진행된다.
1.무작위로 사용자 \(u\)를 선택한 다음 사용자가 클릭한 임의의 품목 \(i\)를 선택한다. 이것이 긍정적 품목이다.
2.사용자가 품목 \(i\)보다 적은 횟수로 클릭한 품목 \(j\)를 임의로 선택한다(클릭한 적이 없는 품목도 포함함). 이것이 부정적 품목이다.
3.사용자 \(u\)와 긍정적 품목 \(i\)에 대한 “점수”, \(p_{ui}\)를 예측하는 방정식을 계산한다. 행렬 분해의 경우 방정식은 \(\mathbf{x}_{u} \cdot \mathbf{y}_{i}\)이다.
4.사용자 \(u\)와 부정적 품목 \(j\)에 대한 점수, \(p_{uj}\)를 예측한다.
5.긍정적 품목과 부정적 품목 점수 간의 차이 \(x_{uij} = p_{ui} - p_{uj}\)를 구한다.
6.이 차이를 시그모이드에 전달하여 확률적 경사 하강법(SGD)에서 모형의 모든 파라미터를 업데이트하기 위한 가중치로 사용한다.
이 방법론을 처음 봤을 때 매우 급진적으로 보였다. 특히 예측하려는 점수 실제 값에 신경을 쓰지 않는 점 말이다. 신경 쓰는 건 사용자가 별로 클릭하지 않은 품목 대비하여 어떤 품목을 자주 클릭했는지 순위를 매기는 부분이다. 따라서 모형은 “순위 매기는 법”을 배우게 된다. :)
다른 느린 방법과 비교하여 표본 추출 기반 접근법을 이용하기 때문에 저자는 모형이 상당히 빠르고 확장 가능하다고 설명한다. 또한, 저자는 BPR이 ROC 곡선 아래 면적(AUC)을 직접적으로 최적화한다고 주장한다. 이는 바람직한 특성일 수 있다. 가장 중요한 건 계산 속도를 크게 저하시키지 않고 부가 정보를 쉽게 추가할 수 있다는 점이다.
순위 학습 - WARP
BPR의 가까운 친족을 꼽자면 근사-순위 쌍 가중 손실(WARP 손실)로서 Weston 등이 쓴 WSABIE: 대량의 어휘로 이미지에 주석 다는 작업의 확장에 처음 소개되었다. WARP는 BPR과 매우 유사하다. 사용자마다 긍정적과 부정적 품목에 대해 표본을 추출하고 두 개의 값을 예측하여 그 차이를 취한다. BPR에서는 이 차이를 가중치로 사용하여 SGD를 업데이트해나갔다. WARP에서는 잘못된 예측을 한 경우, 즉 부정적 품목이 긍정적 품목보다 높은 점수를 가질 경우에만 SGD를 업데이트한다. 잘못 예측하지 않은 경우, 잘못된 예측을 하거나 어떤 지정값에 다다를 때까지 부정적 품목을 계속 추출한다.
WARP 논문 저자는 이러한 절차를 통해 BPR이 수행하는 AUC의 최적화가 정밀도의 최적화로 바뀐다고 주장한다. 이 성질은 대부분의 추천 시스템 목표와 관련 있을 것이고 BPR 손실보다 WARP 손실을 최적화하는 편이 개인적으로도 좋았다. WARP는 두 개의 하이퍼 파라미터를 갖는다. 하나는 예측이 얼마나 틀렸는지 보고 SGD 업데이트 수행할지 결정하는 마진 값이다. 논문에서는 마진 값이 1이므로 SGD 업데이트를 수행하기 위해서는 \(p_{uj} > p_{ui} + 1\)로 추정해야 한다. 다른 하이퍼 파라미터는 현재 사용자를 중단하고 다음 사용자로 넘어가기 전, 잘못된 예측을 얻기 위해 부정적 표본 추출을 얼마나 할지 결정하는 지정 값이다.
해당 표본 추출 방법을 사용할 경우 훈련 초기, 훈련되지 않은 모형의 예측은 잘못되기 쉽기 때문에 WARP가 빠르게 실행된다. 그러나 훈련이 어느 정도 진행된 다음 WARP는 잘못된 예측을 해서 업데이트를 수행할 때까지 많은 품목을 표본 추출하고 예측해야 하기 때문에 느리게 실행된다. 그렇지만 모형에서 잘못된 예측을 얻기 어렵다는 건 좋은 현상인 셈이다.
LightFM
Birchbox 이야기로 돌아가자. numpy와 scipy만 사용해서 부가 정보 적용 가능한 BPR을 구현해봤다. 이 결과물은 매우 느렸고 그즈음에 Lyst 사람들이 LightFM 패키지를 공개했다. LightFM은 Cython으로 작성했고 HOGWILD SGD로 병렬화했다. 이걸 보자마자 내 코드는 당장 폐기 처분했고 LightFM으로 기쁘게 갈아탔다.
LightFM은 위와 동일한 방법을 사용하여 부가 정보를 녹인다. 총 “사용자 벡터”를 사용자 관련 부가 정보 벡터(사용자 “변수”라고 함)의 합산으로 가정하며 품목 또한 비슷하게 다룬다. 위에서 \(\mathbf{x}_u\)와 \(\mathbf{s}_a\), 잠재 벡터의 두 종류를 가정했다. LightFM은 모든 것을 부가 정보 또는 변수로 취급한다. 사용자 \(u\)에 대해 한 개의 특정 사용자 벡터를 구하기 위해서는 해당 사용자에 대한 단일 변수로 원-핫-인코딩을 해줘야 한다.
LightFM을 설치하고 Sketchfab “좋아요” 데이터와 모델 태그를 함께 읽어서 고전적인 ALS를 사용한 이전 게시물보다 LightFM의 결과가 더 나은지 확인해보자.
설치
LightFM은 pypi에 있으므로 pip로 매우 간단하게 설치할 수 있다.
pip install lightfm
Mac 사용자는 불행히도 코드를 병렬로 실행시킬 수 없다. 병렬 처리를 사용하려면 brew로 설치 가능한 gcc가 먼저 있어야 한다.
brew install gcc --without-multilib
유의해라, 30분 정도 걸린다. 꼼수를 좀 쓰면 LightFM을 매우 간단하게 설치할 수 있다. 저장소를 먼저 복제하자.
git clone git@github.com:lyst/lightfm.git
그런 다음 setup.py를 열어서 use_openmp라는 변수가 정의된 곳으로 이동한 뒤 True로 설정해라. 그러고 나서 cd lightfm && pip install -e .를 입력해라.
모든 작업이 끝났다면 몇몇 모형을 훈련하기 위해 코드를 작성해보겠다.
데이터 전처리
Sketchfab 데이터를 행렬 형태로 만들기 위해 지난번 사용했던 다수의 함수를 가져와서 rec-a-sketch 저장소 내 helpers.py 파일에 전부 다 집어넣었다.
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy.sparse as sp
from scipy.special import expit
import pickle
import csv
import copy
import itertools
from lightfm import LightFM
import lightfm.evaluation
import sys
sys.path.append('../')
import helpers
df = pd.read_csv('../data/model_likes_anon.psv',
sep='|', quoting=csv.QUOTE_MINIMAL,
quotechar='\\')
df.drop_duplicates(inplace=True)
df.head()
| modelname | mid | uid | |
|---|---|---|---|
| 0 | 3D fanart Noel From Sora no Method | 5dcebcfaedbd4e7b8a27bd1ae55f1ac3 | 7ac1b40648fff523d7220a5d07b04d9b |
| 1 | 3D fanart Noel From Sora no Method | 5dcebcfaedbd4e7b8a27bd1ae55f1ac3 | 2b4ad286afe3369d39f1bb7aa2528bc7 |
| 2 | 3D fanart Noel From Sora no Method | 5dcebcfaedbd4e7b8a27bd1ae55f1ac3 | 1bf0993ebab175a896ac8003bed91b4b |
| 3 | 3D fanart Noel From Sora no Method | 5dcebcfaedbd4e7b8a27bd1ae55f1ac3 | 6484211de8b9a023a7d9ab1641d22e7c |
| 4 | 3D fanart Noel From Sora no Method | 5dcebcfaedbd4e7b8a27bd1ae55f1ac3 | 1109ee298494fbd192e27878432c718a |
# 좋아요 최소 5개 이상인 사용자와 모델만 포함하게 임계 처리한 데이터.
df = helpers.threshold_interactions_df(df, 'uid', 'mid', 5, 5)
최초 좋아요 정보
사용자 수: 62583
모델 개수: 28806
희소 정도: 0.035%
최종 좋아요 정보
사용자 수: 15274
모델 개수: 25655
희소 정도: 0.140%
# 데이터 프레임에서 좋아요 행렬로 변환
# 색인과 ID 매퍼도 만듦.
likes, uid_to_idx, idx_to_uid,\
mid_to_idx, idx_to_mid = helpers.df_to_matrix(df, 'uid', 'mid')
likes
<15274x25655 sparse matrix of type '<class 'numpy.float64'>'
with 547477 stored elements in Compressed Sparse Row format>
train, test, user_index = helpers.train_test_split(likes, 5, fraction=0.2)
지난번과 다른, 특이한 점 하나는 시험 데이터 안에 데이터가 있는 사용자만 포함하도록 훈련 데이터를 만드는 것이다. 이는 LightFM의 내장 precision_at_k 함수를 사용하기 때문에 생기는 일이다.
eval_train = train.copy()
non_eval_users = list(set(range(train.shape[0])) - set(user_index))
eval_train = eval_train.tolil()
for u in non_eval_users:
eval_train[u, :] = 0.0
eval_train = eval_train.tocsr()
이제 Sketchfab 모델에 관련된 모든 부가 정보를 원-핫-인코딩하려고 한다. 이 정보에는 각 모델과 관련한 카테고리 및 태그가 포함되어 있다. 이 정보를 인코딩하는 가장 간단한 방법은 scikit-learn의 DictVectorizer 클래스를 사용하는 것이다. DictVectorizer는 변수 이름을 키로, 가중치를 값으로 담고 있는 딕셔너리들, 그 딕셔너리들의 리스트를 사용한다. 여기서 각 가중치는 1이라고 가정하고 태그 유형과 값의 조합을 키로 취한다.
sideinfo = pd.read_csv('../data/model_feats.psv',
sep='|', quoting=csv.QUOTE_MINIMAL,
quotechar='\\')
sideinfo.head()
| mid | type | value | |
|---|---|---|---|
| 0 | 5dcebcfaedbd4e7b8a27bd1ae55f1ac3 | category | Characters |
| 1 | 5dcebcfaedbd4e7b8a27bd1ae55f1ac3 | category | Gaming |
| 2 | 5dcebcfaedbd4e7b8a27bd1ae55f1ac3 | tag | 3dsmax |
| 3 | 5dcebcfaedbd4e7b8a27bd1ae55f1ac3 | tag | noel |
| 4 | 5dcebcfaedbd4e7b8a27bd1ae55f1ac3 | tag | loli |
# 판다스 groupby로 아마 깔끔하게 처리할 수 있을 거다
# 그러나 그렇게 처리하지 못했다 :(
# 변수들을 포함한 딕셔너리 리스트 만듦
# idx_to_mid와 동일한 순서로 가중치를 부여한다.
feat_dlist = [{} for _ in idx_to_mid]
for idx, row in sideinfo.iterrows():
feat_key = '{}_{}'.format(row.type, str(row.value).lower())
idx = mid_to_idx.get(row.mid)
if idx is not None:
feat_dlist[idx][feat_key] = 1
feat_dlist[0]
{'category_characters': 1,
'category_gaming': 1,
'tag_3d': 1,
'tag_3dcellshade': 1,
'tag_3dsmax': 1,
'tag_anime': 1,
'tag_girl': 1,
'tag_loli': 1,
'tag_noel': 1,
'tag_soranomethod': 1}
from sklearn.feature_extraction import DictVectorizer
dv = DictVectorizer()
item_features = dv.fit_transform(feat_dlist)
item_features
<25655x20352 sparse matrix of type '<class 'numpy.float64'>'
with 161510 stored elements in Compressed Sparse Row format>
이제 item_features 행렬을 갖게 되었다. 각 행은 (likes 행렬의 열과 같은 순서로) 고유 품목이고 각 열은 고유 태그이다. 20352개의 고유 태그가 있는 것 같다.
훈련
품목 변수는 일단 무시하고 기본 설정만 이용하여 LightFM을 WARP로 간단히 실행해보자. BPR을 돌려서 크게 성공했던 적이 없기에 WARP에만 집중할 것이다. 학습 곡선을 계산할 조그만 함수를 만들어보자.
def print_log(row, header=False, spacing=12):
top = ''
middle = ''
bottom = ''
for r in row:
top += '+{}'.format('-'*spacing)
if isinstance(r, str):
middle += '| {0:^{1}} '.format(r, spacing-2)
elif isinstance(r, int):
middle += '| {0:^{1}} '.format(r, spacing-2)
elif (isinstance(r, float)
or isinstance(r, np.float32)
or isinstance(r, np.float64)):
middle += '| {0:^{1}.5f} '.format(r, spacing-2)
bottom += '+{}'.format('='*spacing)
top += '+'
middle += '|'
bottom += '+'
if header:
print(top)
print(middle)
print(bottom)
else:
print(middle)
print(top)
def patk_learning_curve(model, train, test, eval_train,
iterarray, user_features=None,
item_features=None, k=5,
**fit_params):
old_epoch = 0
train_patk = []
test_patk = []
headers = ['Epoch', 'train p@5', 'test p@5']
print_log(headers, header=True)
for epoch in iterarray:
more = epoch - old_epoch
model.fit_partial(train, user_features=user_features,
item_features=item_features,
epochs=more, **fit_params)
this_test = lightfm.evaluation.precision_at_k(model, test, train_interactions=None, k=k)
this_train = lightfm.evaluation.precision_at_k(model, eval_train, train_interactions=None, k=k)
train_patk.append(np.mean(this_train))
test_patk.append(np.mean(this_test))
row = [epoch, train_patk[-1], test_patk[-1]]
print_log(row)
return model, train_patk, test_patk
model = LightFM(loss='warp', random_state=2016)
# 모형 초기화.
model.fit(train, epochs=0);
iterarray = range(10, 110, 10)
model, train_patk, test_patk = patk_learning_curve(
model, train, test, eval_train, iterarray, k=5, **{'num_threads': 4}
)
+------------+------------+------------+
| Epoch | train p@5 | test p@5 |
+============+============+============+
| 10 | 0.14303 | 0.02541 |
+------------+------------+------------+
| 20 | 0.16267 | 0.02947 |
+------------+------------+------------+
| 30 | 0.16876 | 0.03183 |
+------------+------------+------------+
| 40 | 0.17282 | 0.03294 |
+------------+------------+------------+
| 50 | 0.17701 | 0.03333 |
+------------+------------+------------+
| 60 | 0.17872 | 0.03287 |
+------------+------------+------------+
| 70 | 0.17583 | 0.03333 |
+------------+------------+------------+
| 80 | 0.17793 | 0.03386 |
+------------+------------+------------+
| 90 | 0.17479 | 0.03392 |
+------------+------------+------------+
| 100 | 0.17656 | 0.03301 |
+------------+------------+------------+
import seaborn as sns
sns.set_style('white')
def plot_patk(iterarray, patk,
title, k=5):
plt.plot(iterarray, patk);
plt.title(title, fontsize=20);
plt.xlabel('Epochs', fontsize=24);
plt.ylabel('p@{}'.format(k), fontsize=24);
plt.xticks(fontsize=14);
plt.yticks(fontsize=14);
# 훈련 셋을 왼쪽에 그린다
ax = plt.subplot(1, 2, 1)
fig = ax.get_figure();
sns.despine(fig);
plot_patk(iterarray, train_patk,
'Train', k=5)
# 시험 셋을 오른쪽에 그린다
ax = plt.subplot(1, 2, 2)
fig = ax.get_figure();
sns.despine(fig);
plot_patk(iterarray, test_patk,
'Test', k=5)
plt.tight_layout();
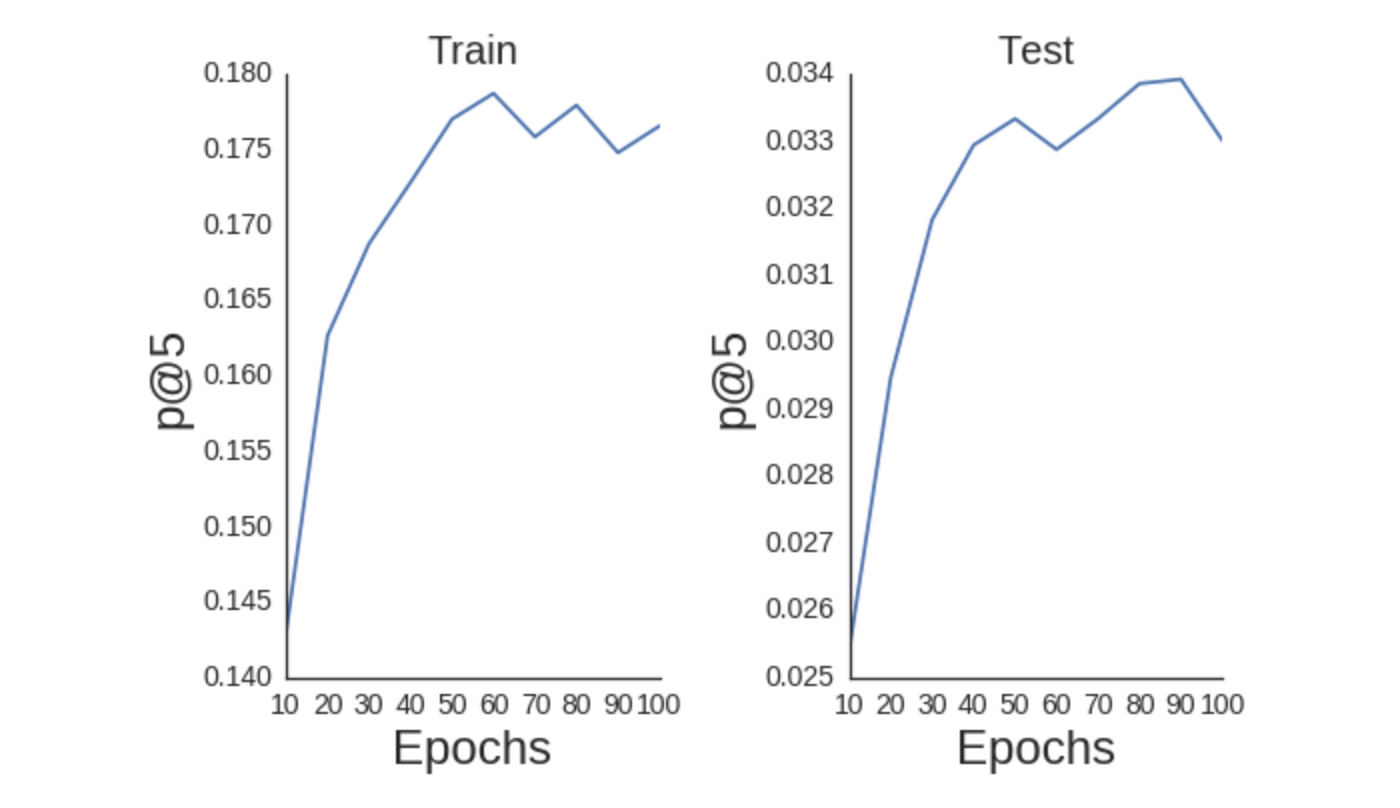
scikit-optimize로 하이퍼 파라미터 최적화하기
기초선을 구했으므로 최적 하이퍼 파라미터를 찾아 p@k 값을 최대로 만들자. 사족으로 모든 상호 작용이 이진 값일 때 k까지의 정밀도가 사용해야 할 가장 좋은 척도인지 모르겠지만 일단 지금은 무시하자…
이전 게시물은 수많은 하이퍼 파라미터에 대해 격자 탐색을 진행했으며 아주 오랜 시간이 걸렸다. 무작위 탐색이 명시적인 격자 탐색보다 낫지만 더 좋은 방법이 있다. scikit-optimize (skopt) 라이브러리를 사용해보자. p@k을 최대화하기 위해 하이퍼 파라미터를 탐색 대상의 자유 매개 변수로 설정하여 블랙박스 최적화 알고리즘을 이용해볼 수 있다. 선택 가능한 최적화 알고리즘이 많이 있지만 오늘은 forest_minimize만 사용해볼 것이다.
설정은 매우 간단하다. 먼저 최소화하려는 목적 함수를 정의해야 한다. 목적 함수는 해를 구하고자 하는 매개 변수를 인자로 받아 해당 매개 변숫값에 대한 목적 함수의 값을 반환한다. 우리 사례에 적용해보면 하이퍼 파라미터를 전달하여 해당 파라미터로 LightFM 모형을 훈련시킨 다음 훈련 결과를 p@k로 평가, 반환하는 작업이다. 목적 함수를 최소화해야 하므로 p@k의 음수를 반환해야 한다. p@k를 최대화하는 것은 p@k의 음수를 최소화하는 것과 동일하기 때문이다. 마지막으로 목적 함수에 하이퍼 파라미터를 전달할 수 있게 전역 변수를 자유롭게 사용하게끔 코드를 작성해야 한다.
from skopt import forest_minimize
def objective(params):
# 언패킹 하기
epochs, learning_rate,\
no_components, alpha = params
user_alpha = alpha
item_alpha = alpha
model = LightFM(loss='warp',
random_state=2016,
learning_rate=learning_rate,
no_components=no_components,
user_alpha=user_alpha,
item_alpha=item_alpha)
model.fit(train, epochs=epochs,
num_threads=4, verbose=True)
patks = lightfm.evaluation.precision_at_k(model, test,
train_interactions=None,
k=5, num_threads=4)
mapatk = np.mean(patks)
# 목적 함수 최소화하기를 원하므로 음수로 만들기
out = -mapatk
# 진행 중 발생할 수 있는 이상 수치 값 처리하기
if np.abs(out + 1) < 0.01 or out < -1.0:
return 0.0
else:
return out
목적 함수를 정의했으니 하이퍼 파라미터의 범위를 정의해보자. 단순하게 최솟값과 최댓값을 줄 수도 있고 아래처럼 분포를 가정해볼 수 있다. 정의한 범위로 forest_minimize를 간단히 호출한 뒤 조금 오래 기다려보자.
space = [(1, 260), # epochs
(10**-4, 1.0, 'log-uniform'), # learning_rate
(20, 200), # no_components
(10**-6, 10**-1, 'log-uniform'), # alpha
]
res_fm = forest_minimize(objective, space, n_calls=250,
random_state=0,
verbose=True)
print('찾아낸 p@k 최댓값: {:6.5f}'.format(-res_fm.fun))
print('최적 파라미터:')
params = ['epochs', 'learning_rate', 'no_components', 'alpha']
for (p, x_) in zip(params, res_fm.x):
print('{}: {}'.format(p, x_))
찾아낸 p@k 최댓값: 0.04781
최적 파라미터:
epochs: 168
learning_rate: 0.09126423099690231
no_components: 104
alpha: 0.00023540795300720628
꽤 괜찮다! 하이퍼 파라미터 기본값을 사용하여 ~ 0.034의 p@k로 시작한 다음 더 나은 값을 찾아가면서 0.0478로 증가시켰다. 행렬 분해 모형에 품목 변수를 부가 정보로 녹이면 어떤 일이 발생하는지 한번 보자.
순위 학습 + 부가 정보
LightFM은 부가 정보 전달 여부와 상관없이 작은 가정 하나를 세운다. user_features 또는 item_features를 직접 전달하지 않으면 LightFM은 두 변수 행렬이 사용자 및 품목 변수 행렬의 크기 (num_users X num_users)와 (num_items X num_items)인 항등 행렬이라고 가정한다. 이 작업을 효과적으로 수행하는 방법은 사용자와 품목 ID를 각각 단일한 변수 벡터로 원-핫-인코딩하는 것이다. item_features 행렬을 직접 전달하면 LightFM은 원-핫-인코딩을 수행하지 않는다. 따라서 명시적으로 정의하지 않는 한 사용자와 품목 ID는 그 자체로 고유한 벡터를 갖지 않는다. 이 문제를 해결하는 가장 쉬운 방법은 항등 행렬을 생성한 다음 미리 만든 item_features 행렬 옆으로 붙이는 것이다. 이 방법을 통해 각 품목은 고유 ID에 대한 단일 벡터와 태그들에 대한 벡터 집합으로 표현이 된다.
# item_features를 수평으로 쌓는 작업이 필요
eye = sp.eye(item_features.shape[0], item_features.shape[0]).tocsr()
item_features_concat = sp.hstack((eye, item_features))
item_features_concat = item_features_concat.tocsr().astype(np.float32)
이제 item_features를 포함시킨 새 목적 함수를 정의해보자.
def objective_wsideinfo(params):
# 언패킹 하기
epochs, learning_rate,\
no_components, item_alpha,\
scale = params
user_alpha = item_alpha * scale
model = LightFM(loss='warp',
random_state=2016,
learning_rate=learning_rate,
no_components=no_components,
user_alpha=user_alpha,
item_alpha=item_alpha)
model.fit(train, epochs=epochs,
item_features=item_features_concat,
num_threads=4, verbose=True)
patks = lightfm.evaluation.precision_at_k(model, test,
item_features=item_features_concat,
train_interactions=None,
k=5, num_threads=3)
mapatk = np.mean(patks)
# 목적 함수 최소화하기 원하므로 음수로 만들기
out = -mapatk
# 진행 중 발생할 수 있는 이상 수치 값 처리하기
if np.abs(out + 1) < 0.01 or out < -1.0:
return 0.0
else:
return out
위에서 정의한 대로 하이퍼 파라미터 탐색을 새로 실행해보자. 사용자와 품목 정규화(알파) 항 간의 비율을 제어하는 별도의 크기 조정 파라미터를 추가하겠다. 별도로 추가한 품목 변수들에 대해 각기 다른 수준의 규제를 적용해볼 수 있다. 또한 forest_minimization에 x0 항을 입력하여 부가 정보가 없었던 이전 실행 때의 최적 파라미터에서 하이퍼 파라미터 탐색을 시작할 수 있다.
space = [(1, 260), # epochs
(10**-3, 1.0, 'log-uniform'), # learning_rate
(20, 200), # no_components
(10**-5, 10**-3, 'log-uniform'), # item_alpha
(0.001, 1., 'log-uniform') # user_scaling
]
x0 = res_fm.x.append(1.)
# 형 변환이 필요하다
item_features = item_features.astype(np.float32)
res_fm_itemfeat = forest_minimize(objective_wsideinfo, space, n_calls=50,
x0=x0,
random_state=0,
verbose=True)
print('찾아낸 p@k 최댓값: {:6.5f}'.format(-res_fm_itemfeat.fun))
print('최적 파라미터:')
params = ['epochs', 'learning_rate', 'no_components', 'item_alpha', 'scaling']
for (p, x_) in zip(params, res_fm_itemfeat.x):
print('{}: {}'.format(p, x_))
찾아낸 p@k 최댓값: 0.04610
최적 파라미터:
epochs: 192
learning_rate: 0.06676184785227865
no_components: 86
item_alpha: 0.0005563892936299544
scaling: 0.6960826359109953
“더 안 좋은 p@k를 얻으려고 이 모든 일을 여태 벌인거야?”라고 생각할 수 있다. 솔직히 말하자면 몹시 좌절스럽다. 예전에도 이런 문제가 발생하는 걸 본 적이 있다. 보고자 하는 평가 척도가 뭐든 간에 부가 정보를 추가하면 종종 그 값이 낮아지거나 비슷한 수준이고는 했다. 사실 공정성 측면에서 기본 최적화의 경우 250회 호출을 진행했으나 위의 최적화에서는 50회 호출을 진행했다. 이는 행렬 분해 모형이 사용자와 품목의 숫자만큼 확장되어 훨씬 느리게 학습되기 때문이다.
결과가 더 나쁠 수 있는 또 다른 이유가 있다. 어쩌면 사용자의 행동이 사람이 정의한 태그와 카테고리보다 훨씬 좋은 정보일 수 있다. 일부 모델의 경우 태그 정보 품질이 안 좋을 수 있다. 또한 더 나은 결과를 얻기 위해, 말하자면 별도의 정규화 항을 이용해서 ID의 고유 벡터와 비교하여 태그 크기를 다르게 조정해야 할 수도 있다. 어쩌면 태그 숫자만큼 각 태그의 가중치를 규제해야 할 수도 있다. 최소 X개의 모델에서 태그를 사용하지 않는 한 태그를 포함시키면 안 되는 것일지도 모른다. 콜드 스타트 문제를 해결하기 위해 사용자 상호 작용이 거의 없는 모델에서만 태그를 적용해야 하는 걸지도 모른다. 누구 아는 사람?! 직접 실험해보는 걸 좋아하지만 다른 사람의 경험 또한 기꺼이 듣고 싶다.
재미로 변수 임베딩 하기
이 모든 것과 상관없이 품목 변수를 녹여 사용할 경우 이점은 분명 존재한다. 사용자 및 품목과 동일한 공간에 임베드시킨 벡터가 있기에 추천을 다양하게 해 볼 수 있다. 먼저 최적 파라미터를 사용하여 전체 데이터셋에서 모형을 다시 학습시켜보자.
epochs, learning_rate,\
no_components, item_alpha,\
scale = res_fm_itemfeat.x
user_alpha = item_alpha * scale
model = LightFM(loss='warp',
random_state=2016,
learning_rate=learning_rate,
no_components=no_components,
user_alpha=user_alpha,
item_alpha=item_alpha)
model.fit(likes, epochs=epochs,
item_features=item_features_concat,
num_threads=4)
변수 정렬하기
Sketchfab을 사용하고 있고 Google의 틸트 브러시 VR 응용 프로그램으로 만든 모델에 달리는 태그 틸트 브러시를 클릭했다고 가정해보자. Sketchfab은 어떤 결과를 보여줄까? 현재 모델의 “틸트 브러시스러움”과는 아마 상관없이 품목 인기도를 기반으로 결과를 보여줄 거다. 요인화한 태그를 이용하여 해당 유사도를 정렬하는 방식으로 틸트 브러시 태그와 가장 비슷한 모델 목록을 보여줄 수 있다. 이를 위해 틸트 브러시 벡터를 찾아 모든 모델에 대해 코사인 유사도를 계산하자.
item_features 행렬 왼쪽에 ID 행렬을 추가했음을 기억해라. 이는 item_features 행렬 열 색인과 품목 변수를 매핑한 DictVectorizer에 품목 숫자만큼 색인이 빠져있음을 의미한다.
idx = dv.vocabulary_['tag_tiltbrush'] + item_features.shape[0]
다음으로 틸트 브러시 벡터와 모든 품목 표현 간의 코사인 유사도를 계산할 필요가 있다. 여기서 각 품목 표현은 변수 벡터의 총합이다. 이 변수 벡터들은 LightFM 모형에서 item_embeddings로 저장된다. (참고: 세부적으로 LightFM 모형에 편향 항이 존재하나 지금은 일단 무시하고 있다.)
def cosine_similarity(vec, mat):
sim = vec.dot(mat.T)
matnorm = np.linalg.norm(mat, axis=1)
vecnorm = np.linalg.norm(vec)
return np.squeeze(sim / matnorm / vecnorm)
tilt_vec = model.item_embeddings[[idx], :]
item_representations = item_features_concat.dot(model.item_embeddings)
sims = cosine_similarity(tilt_vec, item_representations)
마지막으로 틸트 브러시 벡터와 가장 유사한 상위 5개의 Sketchfab 모델 섬네일을 시각화하기 위해 이전 블로그 게시물의 일부 코드를 재사용했다.
import requests
def get_thumbnails(row, idx_to_mid, N=10):
thumbs = []
mids = []
for x in np.argsort(-row)[:N]:
response = requests.get('https://sketchfab.com/i/models/{}'\
.format(idx_to_mid[x])).json()
thumb = [x['url'] for x in response['thumbnails']['images']
if x['width'] == 200 and x['height']==200]
if not thumb:
print('no thumbnail')
else:
thumb = thumb[0]
thumbs.append(thumb)
mids.append(idx_to_mid[x])
return thumbs, mids
from IPython.display import display, HTML
def display_thumbs(thumbs, mids, N=5):
thumb_html = "<a href='{}' target='_blank'>\
<img style='width: 160px; margin: 0px; \
border: 1px solid black;' \
src='{}' /></a>"
images = ''
for url, mid in zip(thumbs[0:N], mids[0:N]):
link = 'http://sketchfab.com/models/{}'.format(mid)
images += thumb_html.format(link, url)
display(HTML(images))
display_thumbs(*get_thumbnails(sims, idx_to_mid))





제법 괜찮다! 이들 각각은 틸트 브러시로 만들어진 것처럼 보인다. 위 이미지를 클릭하여 Sketchfab 웹 사이트의 모델을 직접 확인해봐라.
그밖에 무얼 또 해볼 수 있을까?
태그 제안
Sketchfab에서 사람들이 태그를 더 많이 사용하게끔 유도하고자 한다고 가정해보자. 이는 사용자 참여를 이끔과 동시에 사용자에게 구조화 데이터를 만드는 작업을 공짜로 시킬 수 있기에 회사에게 큰 이익이다. Sketchfab의 경우 이미지와 함께 연관 태그를 제안함으로써 이러한 행동을 장려할 수 있다. 시도해볼 만한 방법 중 한 가지는 모델에 현재 달리지 않은 태그를 제안하는 것이다. 여기엔 모델과 가장 유사한 태그 벡터를 찾은 다음 이미 존재하는 태그를 제외시키는 작업이 포함된다.
idx = 900
mid = idx_to_mid[idx]
def display_single(mid):
"""모델 1개의 섬네일 보여주기"""
response = requests.get('https://sketchfab.com/i/models/{}'\
.format(mid)).json()
thumb = [x['url'] for x in response['thumbnails']['images']
if x['width'] == 200 and x['height']==200][0]
thumb_html = "<a href='{}' target='_blank'>\
<img style='width: 200px; margin: 0px; \
border: 1px solid black;' \
src='{}' /></a>"
link = 'http://sketchfab.com/models/{}'.format(mid)
display(HTML(thumb_html.format(link, thumb)))
display_single(mid)
# 변수 색인과 변수 이름을 연결하는 매퍼 만들기
idx_to_feat = {v: k for (k, v) in dv.vocabulary_.items()}
print('태그:')
for i in item_features.getrow(idx).indices:
print('- {}'.format(idx_to_feat[i]))

태그:
- category_architecture
- category_characters
- category_cultural heritage
- category_products & technology
- category_science, nature & education
- tag_rock
- tag_sculpture
- tag_woman
# 모든 태그 벡터의 색인
tag_indices = set(v for (k, v) in dv.vocabulary_.items()
if k.startswith('tag_'))
# 이미 있는 태그
filter_tags = set(i for i in item_features.getrow(idx).indices)
item_representation = item_features_concat[idx, :].dot(model.item_embeddings)
sims = cosine_similarity(item_representation, model.item_embeddings)
suggested_tags = []
i = 0
recs = np.argsort(-sims)
n_items = item_features.shape[0]
while len(suggested_tags) < 10:
offset_idx = recs[i] - n_items
if offset_idx in tag_indices\
and offset_idx not in filter_tags:
suggested_tags.append(idx_to_feat[offset_idx])
i += 1
print('제안하는 태그:')
for t in suggested_tags:
print('- {}'.format(t))
제안하는 태그:
- tag_greek
- tag_castel
- tag_santangelo
- tag_eros
- tag_humanti
- tag_galleria
- tag_batholith
- tag_rome
- tag_substanced880
- tag_roman
빠른 결론
게시물이 길었다. 수행해야 할 학습도 많았고 최적화시킬 파라미터도 많았다. 성능에 대해서는 지난 게시물의 ALS 모형을 이기기 어려웠다고 말해두고 싶다. 예전 모형은 최적화시킬 파라미터가 더 적고 최적 하이퍼 파라미터에서 모형이 좀 벗어나도 훨씬 “용인되는” 편이다. SGD는 그와 반대로 학습률이 작다면 쓸모없는 결과만 내놓을 것이다. 그러나 탐색에 충분한 시간을 들인다면 ALS를 능가하는 것도 가능하다. 또한 부가 정보를 녹일 수 있는 기능은 새로운 유형의 추천을 만들고 콜드 스타트 문제를 해결할 때 특히 요긴하다. 따라서 시도해볼 만한 모형 후보에 추가해놓는 걸 추천한다.
Subscribe via RSS
