Xinran He, Junfeng Pan, Ou Jin, Tianbing Xu, Bo Liu, Tao Xu, Yanxin Shi, Antoine Atallah, Ralf Herbrich, Stuart Bowers, Joaquin Quiñonero Candela의 Practical Lessons from Predicting Clicks on Ads at Facebook을 번역했습니다.

초록

온라인 광고에서 광고주는 광고 클릭 같이 측정 가능한 사용자 응답에 대해 입찰하며 대금을 지불한다. 그러므로 클릭 예측 시스템은 온라인 광고 시스템의 핵심이다. 매일 활동 중인 7억 5천만 명 이상의 사용자와 1백만 명 이상의 유효 광고주를 고려할 때 Facebook 광고 클릭을 예측하는 일은 상당히 어려운 기계학습 작업이다. 이 논문은 결정 트리와 로지스틱 회귀를 결합한 모형을 소개하며 해당 모형은 시스템 성능에 전반적으로 큰 영향을 미치면서 결정 트리 또는 로지스틱 회귀 하나만 사용한 것보다 예측 성능이 3% 이상 향상했다. 다음으로 몇 개의 기본 매개변수가 시스템 최종 예측 성능에 미치는 영향을 조사했다. 당연한 말이지만 가장 중요한 건 적절한 변수를 찾는 일이다. 사용자나 광고 이력 정보를 담은 변수는 다른 유형의 변수보다 훨씬 중요하다. 적절한 변수와 적절한 모형(의사 결정 트리 및 로지스틱 회귀)을 갖춘 다음에야 다른 요인들이 작게 기여한다(개선폭이 작더라도 규모 확장을 고려한다면 중요하다). 데이터 신선도, 학습률 체계와 데이터 샘플링에 대해 최적 처리 방법을 적용하면 모형 성능이 다소 향상할 수 있으나 매우 값진 변수를 추가하거나 적절한 모형을 처음부터 선택하는 것보다 그 중요도는 훨씬 못하다.

1. 개론

디지털 광고 업계는 수십억 달러 규모이며 매년 급격히 커지고 있다. 온라인 광고 플랫폼 대부분은 광고를 동적으로 할당하며 사용자 관심도에 따라 조정한다. 광고 후보에 대한 사용자의 예상 효용 계산하는 일에 기계학습이 중점적인 역할을 하며 이런 방식을 통해 시장 효율성은 높아진다.

Varian과 Edelman 등이 쓴 2007년경 논문들은 Google과 Yahoo!가 개척한 클릭마다 입찰하고 지불하는 경매 시스템에 대해 설명한다. 같은 해 Microsoft는 동일한 경매 모형을 기반으로 스폰서 검색 시장을 구축했다. 광고 입찰의 효율성은 클릭 예측의 정확도 및 보정에 달려있다. 클릭 예측 시스템은 견고하고 적응력이 있어야 하며 대량의 데이터를 학습시킬 수 있어야 한다. 본 논문의 목표는 이런 요구 사항을 염두에 두고 실제 데이터로 수행한 실험에서 얻은 통찰을 공유하는 일이다.

스폰서 검색 광고는 사용자 질의를 명시적 또는 암시적으로 질의와 일치하는 광고 후보를 검색하는 데 사용한다. Facebook은 광고를 검색어와 연결하진 않았지만 인구 통계 및 관심 분야를 이용해 타겟팅한다. 따라서 사용자가 Facebook을 방문할 경우 표시 가능한 광고의 양은 스폰서 검색보다 많을 수 있다.

사용자가 Facebook을 방문할 때 광고 게재가 요청되며 요청마다 매우 많은 수의 광고 후보를 처리해야 하기 때문에 먼저 분류기 시리즈를 계산 비용이 증가하는 순서로 만든다. 이 논문은 분류기 시리즈의 마지막 단계이자 광고 최종 후보군에 대해 예측하는 클릭 예측 모형을 중점적으로 다룬다.

결정 트리와 로지스틱 회귀를 결합한 하이브리드 모형은 그중 하나만 사용한 것보다 예측 성능이 3% 이상 향상한다. 이 개선폭은 전체 시스템 성능에 중대한 영향을 미친다. 몇 개의 기본 매개변수가 시스템 최종 예측 성능에 영향을 미친다. 예상대로 가장 중요한 건 적절한 변수를 찾는 일이다. 사용자나 광고 이력 정보를 담은 변수는 다른 유형의 변수보다 훨씬 중요하다. 적절한 변수와 적절한 모형(의사 결정 트리와 로지스틱 회귀)을 갖춘 다음에야 다른 요인들이 작게 기여한다.(개선폭이 작더라도 규모 확장을 고려한다면 중요하다). 데이터 신선도, 학습률 체계와 데이터 샘플링에 대해 최적 처리 방법을 적용하면 모형 성능이 다소 향상할 수 있으나 매우 값진 변수를 추가하거나 적절한 모형을 처음부터 선택하는 것보다 그 중요도는 훨씬 못하다.

2장은 실험 설정에 대한 개요로 시작한다. 3장에서는 여러 가지 확률론적 선형 분류기와 다양한 온라인 학습 알고리즘을 평가한다. 변수 변환과 데이터 신선도 영향력을 평가하기 위해 선형 분류기 관련 내용을 계속 진행한다. 꽤 작은 크기의 모형을 만들면서 데이터 신선도와 온라인 학습 관련한 실제 결과에 특히 영감을 얻어 온라인 학습 계층을 통합한 모형 아키텍처를 제시할 것이다. 4장에서는 온라인 학습 계층의 핵심 구성 요소이자 실시간 훈련 데이터의 실시간 스트림을 생성시킬 수 있는 인프라 속 실험적인 부분, 즉 온라인 조이너에 대해 설명한다.

마지막으로 메모리와 정확도를 교환하여 계산 시간을 산출하고 대규모 훈련 데이터를 다룰 수 있는 방법을 제시한다. 5장은 방대한 규모의 응용 프로그램을 위해 메모리 및 대기 시간을 유지 가능하게 하는 실용적 방법을 설명하고 6장에서는 훈련 데이터 양과 정확도 사이 균형 관계를 조사한다.

2. 실험 설정

엄격하고 통제된 실험을 수행하기 위해 2013년 4분기 중 한 주를 임의로 선택하여 오프라인 훈련 데이터 준비를 했다. 상이한 조건의 훈련 및 테스트 데이터를 동일하게 가져가기 위해 온라인에서 관측한 것과 비슷하게 오프라인 훈련 데이터를 준비했다. 저장한 오프라인 데이터를 훈련과 테스트 용으로 분할하여 온라인 훈련과 예측을 위한 스트리밍 데이터 시뮬레이션 용도로 사용했다. 이 논문 모든 실험에 동일한 훈련/테스트 데이터를 테스트베드로 이용했다.

평가 척도: 기계 학습 모형에 영향을 주는 요인에 가장 큰 관심이 있기 때문에 이익 및 수익과 직접 연관된 지표보다는 예측 정확도를 사용했다. 본 작업에서는 정규화 엔트로피(NE)와 보정을 주요 평가 척도로 사용한다.

정규화 엔트로피, 보다 정확하게 정규화 크로스 엔트로피는 노출 당 평균 로그 손실을 모든 노출에 대해 백그라운드 클릭률(CTR)로 모형이 예측한 경우 평균 로그 손실이 될 값으로 나눈 것과 같다. 즉, 백그라운드 CTR의 엔트로피로 정규화한 예측 로그 손실이다. 백그라운드 CTR은 훈련 데이터셋의 관측된 평균 CTR이다. 척도를 정규화한 로그 손실이라고 보는 게 더 이해하기 쉬울 것이다. 값이 낮을수록 모형 예측력이 좋은 것이다. 정규화한 이유는 백그라운드 CTR이 0 또는 1에 가까울수록 로그 손실을 더 좋게 달성할 수 있기 때문이다. 백그라운드 CTR 엔트로피로 나누면 NE는 백그라운드 CTR에 덜 민감해진다. 주어진 훈련 데이터셋이 레이블 \(y_i \in \{-1, +1\}\)과 예측 클릭 확률 \(p_i, i = 1, 2, … N\)의 \(N\)개 샘플을 가진다고 하자. 관측된 평균 CTR이 \(p\)라면,

(1)
\[NE = {-{1 \over N}\sum_{i=1}^n({1+y_i \over 2} \log(p_i) + {1-y_i \over 2} \log(1 - p_i)) \over -(p * \log(p) + (1-p) * \log(1-p))}\]

NE는 기본적으로 상대 정보 이득(RIG) 계산에 사용하는 구성 요소이며 \(RIG = 1 - NE\)이다.

보정은 평균 예측 CTR과 관측된 CTR 간의 비율이다. 즉, 실제로 관측된 클릭 수에 대한 예측 클릭 수 비율이다. 정확하고 잘 보정된 CTR 예측은 온라인 입찰 및 경매 성공에 필수이므로 보정은 매우 중요한 척도이다. 보정 값이 1과 다르지 않을수록 모형은 더 좋은 것이다. 실험에서는 보정값이 일반적이지 않은 경우에 한해서 언급할 것이다.

보정을 고려하지 않는다면 ROC 아래 면적(AUC) 또한 순위 품질을 측정하는데 꽤 좋은 척도이다. 실제 환경에서는 잠재적인 광고 게재 미달 또는 게재 초과를 피하기 위해 최적 순서를 산출하는 것 대신 예측 자체가 정확하길 기대한다. NE는 예측 적합도를 측정하고 보정을 암시적으로 반영한다. 예를 들어 모형이 과대 예측을 2배로 하고 보정을 위해 전체 배율 0.5를 적용하면 AUC는 동일하지만 해당 NE는 향상된다. 측정 기준에 대한 심도 있는 연구는 논문1을 참조하라.

3. 예측 모형 구조

이 장은 그림 1의 묘사처럼 부스팅 결정 트리와 확률론적 희소 선형 분류기를 연결한 하이브리드 모형 구조를 제시한다. 3.1절은 의사 결정 트리가 확률론적 선형 분류기의 정확도가 상당히 향상하는 매우 강력한 입력 변수 변환 방법임을 설명한다. 3.2절은 훈련 데이터의 신선도가 어떻게 예측의 정확도로 이어지는지 설명한다. 이를 통해 온라인 학습 방법을 선형 분류기 훈련에 적용해볼 아이디어를 얻었다. 3.3절은 확률론적 선형 분류기 두 족(族)에 대한 온라인 학습의 여러 방법을 비교한다.

그림 1

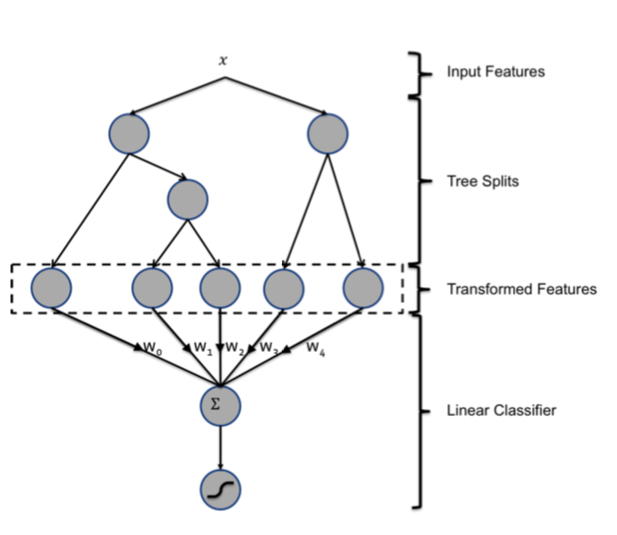
그림 1: 하이브리드 모형 구조. 입력 변수를 부스팅 결정 트리 통해 변환한다. 각 트리의 출력을 희소 선형 분류기에 대한 범주형 입력 변수로 처리한다. 부스팅 결정 트리가 매우 강력한 변수 변환임이 입증됐다.

평가할 온라인 학습 기법은 희소 선형 분류기에 대한 확률적 기울기 하강법(SGD) 알고리즘을 기반으로 한다. 변수 변환 후 광고 노출은 구조화된 벡터

\(\mathbf{x} = (\mathbf{e}_{i_1}, …, \mathbf{e}_{i_n})\)의 함수로 주어진다. 여기서 \(\mathbf{e}_{i}\)는 i번째 단위 벡터이고 \(i_1, … , i_n\)은 n개 범주형 입력 변수를 지칭한다. 클릭함 또는 클릭하지 않음을 나타내는 이진 레이블 \(y \in \{+1, -1\}\)을 훈련 단계에서 갖고 있다고 가정한다.

광고 노출 레이블 \((\mathbf{x}, y)\)이 있을 때 활성 가중치 선형 조합은 다음과 같다.

(2)
\[s(y, \mathbf{x}, \mathbf{w}) = y\cdot\mathbf{w}^T\mathbf{x}=y\sum_{j=1}^n{w_{j,i_{j}}},\]

여기서 \(\mathbf{w}\)는 클릭 선형 점수의 가중치 벡터이다.

논문2에서 저술한 대로 프로빗 회귀분석을 위한 최신 베이지안 온라인 학습 체계(BOPR)는 우도와 사전 확률을 다음과 같이 정의한다.

\[p(y|\mathbf{x}, \mathbf{w}) = \Phi\left({s(y, \mathbf{x}, \mathbf{w}) \over \beta}\right),\] \[p(\mathbf{w}) = \prod_{k=1}^N N(w_k;\mu_k,\sigma_k^2),\]

여기서 \(\Phi(t)\)는 표준 정규 분포의 누적 밀도 함수이고 \(N(t)\)는 표준 정규 분포의 밀도 함수이다.

적률 매칭과 함께 기댓값 전파를 통해 온라인 학습을 진행한다. 가중치 벡터 \(\mathbf{w}\)에 대한 근사 사후 분포의 평균 및 분산으로 결과 모형은 이루어진다. BOPR 알고리즘에서 추론은 \(p(\mathbf{w}|y, \mathbf{x})\)를 계산하고 가장 가깝게 분해되는 \(p(\mathbf{w})\)의 가우시안 근사에 그것을 투영시키는 작업이다. 따라서 갱신 알고리즘은 0이 아닌 \(\mathbf{x}\) 모든 성분의 평균 및 분산에 관한 갱신 방정식만 가지고 표현할 수 있다(논문2 참조).

(3)
\[\mu_{i_j} \leftarrow \mu_{i_j} + y \cdot {\sigma^2_{i_j} \over \Sigma} \cdot v \left({s(y, \mathbf{x}, \mathbf{\mu}) \over \Sigma}\right),\]
(4)
\[\sigma^2_{i_j} \leftarrow \sigma^2_{i_j} \cdot \left[1 - {\sigma^2_{i_j} \over \Sigma^2} \cdot w \left({s(y, \mathbf{x}, \mathbf{\mu}) \over \Sigma}\right)\right],\]
(5)
\[\Sigma^2 = \beta^2 + \sum_{j=1}^n{\sigma^2_{i_j}}.\]

여기서 보정 함수 \(v\)와 \(w\)는 \(v(t):=N(t) / \Phi(t)\)와 \(w(t):= v(t) \cdot [v(t) + t]\)로 정의한다. 이 추론을 신뢰 벡터 \(\mu\)와 \(\sigma\) 기반의 SGD 체계로 볼 수 있다.

BOPR와 우도 함수가

\[p(y|\mathbf{x}, \mathbf{w}) = sigmoid(s(y, \mathbf{x}, \mathbf{w})),\]

인 SGD를 비교해보자. 여기서 \(sigmoid(t) = \exp(t) /(1 + \exp(t))\)이다. 결과 알고리즘을 로지스틱 회귀(LR)라고 부른다. 모형 추론은 로그 우도에 대한 도함수를 계산한 다음 좌표 별 기울기 방향으로 보폭만큼 이동하면서 이루어진다.

(6)
\[w_{i_j} \leftarrow w_{i_j} + y \cdot \eta_{i_j} \cdot g(s(y, \mathbf{x}, \mathbf{w})),\]

여기서 \(g\)는 0이 아닌 모든 성분의 로그 우도에 관한 기울기이고 \(g(s) := [y(y + 1) / 2 - y \cdot sigmoid(s)]\)로 구할 수 있다. 식 (3)을 신뢰 불확실성 \(\sigma\)가 보폭 \(\eta_{i_j}\)을 자동으로 제어하는, (6) 같은 형태의 평균 벡터 \(\mu\)에 관한 좌표 별 기울기 하강법으로 볼 수 있다. 3.3절에서 다양한 보폭 함수 \(\eta\)를 제시하고 BOPR과 비교할 것이다.

위에서 설명한 SGD 기반 LR과 BOPR 모두 훈련 데이터 하나하나에 대해 적응하는 스트림 학습기이다.

3.1 의사 결정 트리 변수 변환

선형 분류기의 입력 변수를 변환하여 정확도가 향상하는 방법은 간단하게 두 가지 있다. 연속형 변수의 경우 비선형 변환을 학습하기 위한 간단한 트릭으로 변수를 구간 별로 나누고 각 구간을 범주형 변수로 처리하는 방법이 있다. 선형 분류기는 변수 구간마다 특정 상수를 대응시켜 비선형 변환을 효과적으로 학습한다. 이때 구간 경계를 효과적으로 정하여 학습하는 것이 중요하며 그를 위한 정보 최대화 기법이 여러 개 존재한다.

간단하지만 효과적인 두 번째 변환 방법은 튜플 입력 변수를 만드는 것이다. 범주형 변수의 경우 완전 탐색 접근법은 카테시안 곱을 모두 취해보는 방식, 즉 원래 변수의 가능한 값 조합을 모든 값으로 갖는 새 범주형 변수를 만드는 방식이다. 모든 조합이 유용하진 않을 것이므로 그런 조합은 제거 가능하다. 입력 변수가 연속형이라면 k-d 트리 같은 것을 사용하여 공동 구간화를 시켜 만들 수 있다.

부스팅 결정 트리는 방금 설명한 종류의 비선형과 튜플 변환을 수행하는 강력하고 편리한 방법이다. 개별 트리는 샘플이 최종 할당되는 리프의 색인을 값으로 취하는 범주형 변수로 볼 수 있다. 이 변수 유형에 대해 1-of-K 코딩을 한다. 예를 들어 하위 트리 총 2개를 갖고 첫 번째 하위 트리가 리프 3개를, 두 번째 하위 트리가 리프 2개를 갖는 그림 1의 부스팅 트리 모형을 생각해보라. 샘플이 첫 번째 하위 트리에서 2번 리프로 끝나고 두 번째 하위 트리에서 1번 리프로 끝나는 경우 선형 분류기에 대한 전체 입력은 이진 값 벡터 \([0, 1, 0, 1, 0]\)가 된다. 여기서 첫 3개의 항목은 첫 번째 하위 트리 리프에, 마지막 2개의 항목은 두 번째 하위 트리 리프에 대응한다. 부스팅 결정 트리 전통적인 \(L_2-TreeBoost\) 알고리즘을 사용하는 Gradient Boosting Machine(GBM)을 적용했다. 각 학습 주기마다 이전 트리들의 잔여분을 모형화하기 위해 새로운 트리를 만든다. 부스팅 결정 트리를 실수 값 벡터를 조밀한 이진 값 벡터로 변환하는 지도 변수 인코딩 기법으로 이해할 수 있다. 루트 노드에서 리프 노드로의 전달은 특정 변수에 대한 규칙을 나타낸다. 이진 값 벡터에 선형 분류기를 적용하는 것은 본질적으로 규칙 집합에 대한 가중치를 학습하는 것이다. 부스팅 결정 트리는 배치 방식으로 학습한다.

선형 모형 입력으로 트리 변수를 사용할 때 효과를 보여주기 위해 실험을 수행했다. 이 실험은 두 가지 로지스틱 회귀 모형을 비교한다. 하나는 트리 변수 변환한 것을 썼고 다른 하나는 일반(변환하지 않은) 변수를 이용했다. 비교를 위해서 부스팅 결정 트리 모형만 사용했다. 표 1에서 결과를 볼 수 있다.

표 1

표 1: 로지스틱 회귀(LR)와 부스팅 결정 트리(Trees)는 강력한 조합을 만든다. 그것의 정규화 엔트로피(NE)를 트리만 사용한 모형과 비교하여 측정했다.

트리 변환을 하지 않은 모형 정규화 엔트로피와 비교해서 트리 변수 변환은 정규화 엔트로피를 3.4% 이상 감소시켰다. 이는 매우 중요한 개선점이다. 참고로 전형적인 피쳐 엔지니어링 실험은 비교 대상 NE를 커봐야 1% 정도 감소시킨다. LR과 트리 모형을 단독으로 사용하면 예측 정확도가 비슷한데(LR이 조금 더 좋음) 조합하는 경우 정확도가 크게 향상된다는 점은 흥미롭다. 유의미한 예측 정확도 향상이다. 참고로 피쳐 엔지니어링 실험 대부분은 정규화 엔트로피를 단지 1퍼센트 이내 감소시킨다.

3.2 데이터 신선도

데이터 분포가 시간이 흐름에 따라 변해가는 동적 환경에 클릭 예측 시스템을 종종 배포한다. 예측 성능에 대한 훈련 데이터 신선도 효과를 알아보았다. 이를 위해 특정일에 모형을 훈련시키고 후속 기간에 테스트를 진행했다. 부스팅 결정 트리 모형과 트리 변환한 입력 변수를 적용한 로지스틱 회귀 모형에 대해 실험했다.

실험은 데이터 하루치로 훈련시키고 6일 연속 평가하며 각 일자마다 정규화 엔트로피를 계산했다. 결과는 그림 2에 나와있다.

그림 2

그림 2: 훈련일로부터 테스트까지 지연된 일수에 관한 예측 정확도. 트리만 사용한 모형으로 6일 지연한 경우 얻은 최저 값으로 정규화 엔트로피를 나눠 정확도를 표시했다.

훈련과 테스트 셋 간 지연 일수가 늘면서 두 모형 모두 예측 정확도가 명백히 떨어진다. 두 모형 모두 주 단위 훈련 대비 일 단위로 훈련시킬 경우 NE가 약 1%까지 감소함을 알 수 있다.

이 결과는 일 단위로 재훈련시킬 값어치가 있음을 알려준다. 옵션 중 하나는 배치를 통해 모형 재훈련시키는 작업을 매일 반복 수행하는 것이다. 부스팅 결정 트리를 재훈련시키는데 필요한 시간은 훈련 샘플 수, 트리 수, 각 트리의 리프 수, CPU, 메모리 등 구성요소에 따라 다르다. 단일 코어 CPU로 수억 개 샘플에 수백 개 트리를 가진 부스팅 모형 만드는 데 24시간 이상 걸릴 수 있다. 현실에서는 전체 훈련 데이터셋을 올리기 위해 메모리 사이즈가 큰 멀티 코어 시스템으로 동시 실행을 통해 몇 시간 내로 훈련을 완료시킬 수 있다. 다음 절에서 대안을 제시한다. 부스팅 결정 트리는 매일 또는 며칠 단위로 훈련시킬 수 있지만 선형 분류기는 온라인 학습을 적용하여 거의 실시간으로 훈련시킬 수 있다.

3.3 온라인 선형 분류기

데이터 신선도를 최대화하기 위해 선형 분류기를 온라인으로, 즉 레이블이 지정된 광고 노출이 발생하자마자 훈련시키는 것도 하나의 옵션이다. 다음 4장에서 실시간 훈련 데이터를 생성할 수 있는 인프라를 설명한다. 이 절에서는 로지스틱 회귀에 대한 SGD 기반 온라인 학습의 학습률 설정 방안 몇 가지를 평가한다. 그런 다음 최선의 방안을 BOPR 모형의 온라인 학습 방법과 비교한다.

(6)의 맥락에서 다음 선택 안을 탐색했다.

1.좌표 별 학습률: \(t\)번째 반복에서 변수 \(i\)에 대한 학습률을 다음과 같이 설정한다.

\[\eta_{t, i} = {\alpha \over \beta + \sqrt{\sum_{j=1}^t{\bigtriangledown_{j, i}^2}}}.\]

여기서 \(\alpha, \beta\)는(논문3에서 제안한) 조정 가능한 매개변수이다.

2.가중치 별 제곱근 학습률:

\[\eta_{t, i} = {\alpha \over \sqrt{n_{t, i}}},\]

여기서 \(n_{t, i}\)는 \(t\)번째 반복까지 변수 \(i\)에 대한 총 훈련 샘플 수이다.

3.가중치 별 학습률:

\[\eta_{t, i} = {\alpha \over n_{t, i}}.\]

4.전역 학습률:

\[\eta_{t, i} = {\alpha \over \sqrt{t}}.\]

5.상수 학습률:

\[\eta_{t, i} = \alpha.\]

처음 세 방법은 학습률을 변수 별로 개별 설정한다. 마지막 두 개는 모든 변수에 동일한 학습률을 사용한다. 조정 가능한 모든 매개 변수는 격자 탐색 기법으로 최적화한다(표 2 참조).

표 2

표 2: 학습률 매개변수

연속적인 학습을 위해 학습률을 0.00001 단위로 낮췄다. 위 학습률 체계를 이용하여 동일 데이터에 LR 모형을 훈련시키고 테스트했다. 실험 결과는 그림 3에 나와있다.

그림 3

그림 3: SGD 사용하는 LR에 대한 다양한 학습률 체계 실험 결과이다. X축은 서로 다른 학습률 체계에 해당한다. 왼쪽 y 주축에 눈금을 그렸고 오른쪽 y 보조축에 표준화 엔트로피를 표시했다.

위 결과에서 좌표 별 학습률을 적용한 SGD가 제일 높은 예측 정확도를 보였고 최저 성능을 기록한 가중치 별 학습률 경우보다 5% NE가 낮았다. 이 결과는 논문3의 결론과 일치한다. 가중치 별 제곱근 또는 상수 학습률을 적용한 SGD의 NE는 비슷하거나 조금 높은 수준이다. 다른 두 체계는 훨씬 안 좋다. 전역 학습률은 각 변수 별 훈련 샘플 수의 불균형으로 주로 실패한다. 각 훈련 샘플은 서로 다른 변수들로 구성될 수 있기에 많이 사용되는 일부 변수는 다른 변수보다 훨씬 많은 훈련 샘플을 취한다. 전역 학습률 체계는 샘플 수가 적은 변수에 관한 학습률이 너무 빨리 감소해서 최적 가중치로 수렴하지 못한다. 가중치 별 학습률 체계는 이런 문제는 없지만 모든 변수의 학습률이 너무 빠르게 감소하기 때문에 역시나 실패한다. 훈련이 너무 일찍 종료되어 모형이 최적이 아닌 지점으로 수렴한다. 이를 통해 이 체계가 모든 방안 중 왜 최저 성능인지 알 수 있다.

흥미로운 건 평균에 대한 BOPR 갱신 방정식 (3)이 LR에 대한 SGD 좌표 별 학습률 버전과 가장 유사하다는 점이다. BOPR의 효과적인 학습률은 각 좌표에 따라 다르며 각 좌표에 연관된 가중치 사후 분산과 모형이 예측한 바와 다른 레이블 “의외성”에 달려있다.

좌표 별 SGD을 적용해 훈련시킨 LR 예측 성능과 BOPR를 비교하기 위해 실험을 수행했다. LR과 BOPR 모형을 동일한 훈련 데이터로 학습시키고 익일 예측 성능을 평가했다. 그 결과는 표 3에 나와있다.

표 3

표 3: 좌표 별 온라인 LR 대 BOPR

아마도 갱신 방정식이 질적으로 유사하다는 점을 고려한다면 BOPR과 좌표 별 학습률 적용한 SGD를 통해 훈련시킨 LR은 NE와 보정(표에 표시되지 않음) 관점에서 예측 성능이 매우 비슷하리라 기대할 수 있다.

BOPR 대비 LR의 한 가지 장점은 평균 및 분산에 비해 각 희소 변수에 관한 가중치만 정하면 되므로 모형 크기가 절반이면 된다는 점이다. 구현에 달려있지만 모형 크기가 작을수록 캐시 지역성은 낫고 캐시 조회는 빨라진다. 예측 시간의 계산 비용 측면에서 LR 모형은 변수 벡터를 가중치 벡터에 대해 내적 한 번만 하면 되지만 BOPR 모형은 변수 벡터를 분산 벡터와 평균 벡터 각각에 대해 두 번 내적 해야 한다.

LR 대비 BOPR의 한 가지 중요한 장점은 베이지안 공식이므로 클릭 확률에 대한 예측 분포가 온전히 제공된다는 점이다. 이를 통해 예측 분포 백분위수를 계산할 수 있으며 탐색 / 획득 학습 체계에 사용할 수 있다.

4. 온라인 데이터 조이너

이전 장에서 더 신선한 훈련 데이터를 사용하면 예측 정확도가 상승한다는 결론을 얻었다. 또 선형 분류기 층을 온라인 학습시키는 간단한 모형 아키텍처를 제시했다.

이 절은 선형 분류기를 온라인 학습으로 훈련시킬 때 사용하는 실시간 학습 데이터를 생성하기 위한 실험적 시스템을 소개한다. 중요한 작업은 온라인 방식으로 훈련 입력(광고 노출)에 레이블(클릭함 / 클릭하지 않음)을 결합하는 것이므로 이 시스템을 “온라인 조이너”라고 부른다. 예컨대 Google 광고 시스템은 유사한 인프라를 스트림 학습에 사용한다. 온라인 조이너는 Scribe라는 인프라에 실시간 훈련 데이터 스트림을 출력한다. 양의 레이블(클릭함)은 잘 정의되어 있는 반면 사용자가 누를 수 있는 “클릭하지 않음” 버튼은 없다. 따라서 사용자가 광고를 본 후 충분히 긴 고정 시간 동안 광고를 클릭하지 않으면 노출을 음의 레이블, 즉 클릭하지 않음으로 간주한다. 대기 시간 창의 길이는 조심스럽게 조정해야 한다.

대기 시간 창을 너무 길게 가지면 실시간 훈련 데이터가 지연되고 클릭 신호를 기다리는 동안 버퍼링 노출에 할당한 메모리가 증가한다. 시간 창이 너무 짧으면 해당 노출은 정리되고 클릭하지 않음으로 분류되면서 클릭 수 중 일부를 잃는다. 이는 ‘클릭률’, 즉 노출에 연관한 총 클릭 수 비율에 부정적인 영향을 준다. 결과적으로 온라인 조이너 시스템은 최신성과 클릭률 사이의 균형을 유지해야 한다.

온전한 클릭률을 갖지 못하기 때문에 실시간 훈련 데이터셋은 편향될 것이다. 기록된 클릭률은 실제의 것보다 다소 낮다. 클릭하지 않음으로 표시한 레이블 일부는 대기 시간이 충분히 길었다면 클릭함 레이블로 매겨졌을 것이기 때문이다. 그러나 사실 관리 가능한 메모리 요구 사항을 만족하는 대기 창 길이를 적용해서 퍼센트 소수점 이하로 편향을 쉽게 줄일 수 있다. 또한 이 작은 편향을 측정해서 교정할 수 있다. 대기 시간 길이와 효율에 대한 더 많은 연구는 논문4에서 찾을 수 있다. 온라인 조이너는 요청 ID를 조인 조건의 기본 구성 요소로 사용하여 광고 노출과 광고 클릭에 관한 분산 스트림 - 스트림 결합을 수행하도록 설계했다. 요청 ID는 사용자가 Facebook에 노출된 콘텐츠의 새로 고침을 작동시키는 행동을 할 때마다 생성된다. 온라인 조이너를 뒤따르는 온라인 학습에 관한 데이터 및 모형 흐름을 도식화하여 그림 4에 나타냈다. 사용자가 Facebook을 방문하고 랭커에 후보 광고를 요청하면 초기 데이터 스트림이 생성된다. 광고는 사용자 기기로 재 전달되며 각 광고와 노출 순위에 사용한 관련 변수가 병렬로 노출 스트림에 추가된다. 사용자가 광고를 클릭하면 해당 클릭이 클릭 스트림에 추가된다. 스트림 대 스트림 조인을 수행하기 위해 시스템은 선입선출 큐를 버퍼 창으로 구성한 해시 큐와 레이블 노출에 대한 고속 랜덤 액세스를 위해 해시 맵을 사용 한다. 일반적으로 해시 큐는 키 - 값 쌍에 대해 세 가지 종류의 작업 즉 인큐, 데큐와 룩업을 수행한다. 예를 들어 항목을 대기열에 인큐 하려면 항목을 대기열 앞에 추가하고 해시 맵에서 대기열 항목 포인터 값으로 키를 만든다. 조인을 위한 창이 온전히 종료된 다음에야 레이블 지정한 노출이 훈련 스트림으로 방출된다. 클릭이 조인되지 않았다면 음의 레이블 샘플로 방출된다.

이 실험 설정에서 훈련기는 훈련 스트림을 통해 지속 학습하고 새 모형을 정기적으로 랭커에 배포한다. 이를 통해 최종적으로 변수 분포 또는 모형 성능 변화를 짧은 시간에 포착, 학습 그리고 교정할 수 있는, 엄격하게 닫힌 작업 순환을 기계 학습 모형 용도로 만들어낸다.

그림 4

그림 4: 온라인 학습 데이터/모형 흐름.

실시간 훈련 데이터 생성 시스템을 실험할 때 중대하게 고려할 점 중 하나는 온라인 학습 시스템을 손상시킬 수 있는 이상치에 대해 보호 메커니즘을 구축해놔야 한다는 점이다. 간단한 예를 들어보자. 일부 데이터 인프라 문제로 인해 클릭 스트림이 즉시성을 점차 잃게 되면 온라인 조이너는 관측된 CTR이 매우 작거나 0인 훈련 데이터를 생성한다. 따라서 실시간 훈련기는 클릭 빈도가 매우 낮거나 0에 가깝게 예측하기 시작한다. 광고 예상 가치는 예상 클릭 확률에 따라 달라지므로 매우 낮은 클릭률(CTR)로 잘못 예측하면 광고 노출 수가 줄어들 수 있다. 이상 탐지 메커니즘이 도움을 줄 수 있다. 예를 들어 실시간 훈련 데이터 분포가 급격히 변하면 온라인 학습기와 온라인 조이너 연결을 자동으로 끊을 수 있다.

5. 메모리와 대기 시간 유지하기

5.1 부스팅 트리의 트리 개수

모형의 트리 개수가 많을수록 예측에 필요한 시간은 길어진다. 이 절은 추정 정확도에 대한 부스팅 트리의 트리 개수 효과를 연구한다.

트리 개수를 1개에서 2,000개까지 증가시키며 하루치 데이터로 모형을 훈련한 후 익일 예측 성능을 테스트했다. 각 트리 리프가 12개가 넘지 않도록 제한했다. 이전 실험과 비슷하게 정규화 엔트로피를 평가 척도로 사용했다. 실험 결과는 그림 5에 나와 있다. 정규화 엔트로피는 부스팅 트리의 트리 개수를 늘리면 줄어든다. 그러나 트리를 추가할 때마다 얻는 한계 이익은 감소한다. 거의 대부분의 NE 개선폭은 첫 500개 트리에서 이뤄졌다. 마지막 트리 1,000개는 NE 0.1% 이하만을 감소시켰다. 또 서브 모형 2에 대한 표준화 엔트로피가 트리 1,000개 이후 점점 다시 증가함을 볼 수 있다. 이런 현상은 과적합 때문에 일어난다. 서브 모형 2에 대한 훈련 데이터는 서브 모형 0과 1의 것보다 4배 적기 때문이다.

그림 5

그림 5: 부스팅 트리 개수에 대한 실험 결과이다. 서로 다른 실선은 서로 다른 서브 모형에 해당한다. X축은 부스팅 트리 개수이다. Y축은 정규화 엔트로피이다.

5.2 부스팅 변수 중요도

변수 개수는 추정 정확도와 계산 성능 간 절충에 영향을 줄 수 있는 또 다른 모형 특징이다. 변수 개수의 영향력을 잘 이해하기 위해 각 변수마다 변수 중요도를 먼저 산출해보았다.

변수 중요도 측정을 목적으로 특정 변수로 인해 손실이 얼마나 누적 감소하는지 잡아내는 통계량, 부스팅 변수 중요도를 사용했다. 각 트리 노드를 구성할 때 제곱 오차를 최대로 감소시키는 최적 변수를 선택하고 분할한다. 한 변수가 여러 트리에서 사용될 수 있으므로 특정 변수에 대한 부스팅 변수 중요도는 모든 트리에서 각 변수가 감소시킨 손실량을 합하여 결정한다.

일반적으로 변수 일부가 설명력 대부분을 갖고 나머지 다수의 변수는 일부분만 기여한다. 누적 변수 중요도 대 변수 개수를 도시할 때 그림 6 같은 패턴을 흔히 볼 수 있다.

그림 6

그림 6: 부스팅 변수 중요도. X축은 변수 개수에 해당한다. 왼쪽 y 주축은 변수 중요도를 로그 척도로 그리고 오른쪽 y 보조축은 누적 변수 중요도를 표시한다.

위 결과에서 상위 10개 변수가 전체 변수 중요도의 약 절반을 차지하는 반면 마지막 300개 변수은 변수 중요도 1% 미만임을 알 수 있다. 이 결과를 바탕으로 상위 10, 20, 50, 100 및 200개 변수만 유지하고 성능이 어떻게 영향을 받는지 평가했다. 실험 결과는 그림 7에 나와있다. 그림에서 변수를 포함시킬수록 표준화 엔트로피의 한계 이익은 비슷한 수준으로 감소함을 볼 수 있다.

그림 7

그림 7: 상위 변수들로 모형을 부스팅 한 결과. 왼쪽 y 주축에 눈금을 그렸고 오른쪽 y 보조축에 표준화 엔트로피를 표시했다.

다음으로 이력과 맥락 변수의 유용성에 대해 탐구할 것이다. 데이터의 본질적으로 민감한 사안과 회사 정책으로 인해 사용한 실제 변수 세부 정보는 공개할 수 없다. 맥락 변수의 일부 예로 현지 시간대, 요일 등이 있다. 이력 변수는 광고에 대한 누적 클릭 수 등이 있다.

5.3 이력 변수

부스팅 모형에서 사용한 변수는 두 가지 유형, 즉 맥락 변수와 이력 변수로 구분할 수 있다. 맥락 변수 값은 사용자가 이용하는 기기 또는 사용자가 현재 이용 중인 페이지처럼 광고를 게재할 맥락과 관련된 최신 정보에 전적으로 의존한다. 반대로 이력 변수는 광고 또는 사용자의 이전 상호 작용(예: 지난주 광고 클릭률 또는 사용자 평균 클릭률)에 따라 달라진다.

이 절은 두 유형 변수에 시스템 성능이 어떻게 의존하는지 탐구한다. 우선 두 유형 변수의 상대적 중요도를 확인했다. 모든 변수를 중요도에 따라 정렬한 다음 상위 k개 중요 변수 중 이력 변수의 비율을 계산했다. 결과는 그림 8에 나와있다. 이력 변수가 맥락 변수보다 훨씬 더 많은 설명력을 제공한다는 걸 결과에서 볼 수 있다. 중요도에 따른 상위 10개 변수는 모두 이력 변수이다. 상위 20개 변수 중 이력 변수 비중은 약 75%인 반면 맥락 변수는 2개뿐이다. 각 유형 변수의 상대적인 가치를 전반적으로 더 잘 이해하기 위해 맥락 변수와 이력 변수만 사용해서 두 개의 부스팅 모형을 학습시킨 다음 두 모형을 변수 모두 사용한 전체 모형과 비교했다. 그 결과가 표 4이다.

그림 8

그림 8: 이력 변수 비율에 대한 결과. X축은 변수 개수에 해당한다. Y축은 상위 k개 중요 변수 중 이력 변수의 비율을 나타낸다.

표 4

표 4: 서로 다른 변수 유형을 사용한 부스팅 모형

표에서 이력 변수가 맥락 변수보다 전반적으로 더 중요한 역할을 한다는 사실을 다시 확인할 수 있다.

이력 변수가 없으면 예측 정확도는 4.5% 감소한다. 반대로 맥락 변수가 없으면 예측 정확도가 1% 미만 떨어진다.

콜드 스타트 문제를 처리하기 위해서 맥락 변수가 매우 중요하다는 점을 알아야 한다. 신규 사용자와 광고의 경우 클릭률 예측에 맥락 변수는 필수적이다.

다음 단계로 이력 변수만 또는 맥락 변수만 사용하여 이어지는 주간에 대해 모형을 훈련시킨 후 그 평가 결과로 데이터 신선도에 대한 변수 종속성을 테스트했다. 결과는 그림 9에 나와있다.

그림 9

그림 9: 서로 다른 변수 유형에 대한 데이터 신선도 결과. X축은 평가 기간이고 y축은 정규화 엔트로피이다.

그림에서 볼 수 있듯이 맥락 변수를 사용한 모형이 이력 변수를 사용한 것보다 데이터 신선도에 더 많이 의존한다. 이력 변수는 사용자 행동을 오랜 기간 축적해서 표현하기에 이 결과가 직관적으로 옳음을 알 수 있다.

6. 대규모 훈련 데이터 다루기

Facebook 광고 노출 데이터 하루치는 엄청난 양의 샘플을 포함할 수 있다. 실제 수치는 기밀사항이므로 밝힐 수 없다. 그러나 하루 분량의 데이터 중 일부만 취해도 수억 개의 샘플일 수 있다. 훈련 비용을 관리하기 위해 일반적으로 사용하는 기법은 훈련 데이터 규모를 줄이는 것이다. 이 절은 균일한 서브 샘플링과 음의 레이블에 대한 다운 샘플링, 즉 데이터를 다운 샘플링하는 두 가지 기법을 평가한다. 각각의 경우에 대해 600개의 트리를 가진 부스팅 트리 모형 집합을 훈련시키고 보정과 정규화 엔트로피 모두 써서 평가를 진행했다.

6.1 균일한 서브 샘플링

훈련 데이터 행에 대한 균일한 서브 샘플링은 구현하기 쉽고 결과 모형을 서브 샘플링한 훈련 데이터와 서브 샘플링하지 않은 테스트 데이터 양측에 수정 없이 사용할 수 있기에 데이터 크기를 줄이기 위한 유용한 접근 방법이다. 대략 기하급수적으로 증가하는 서브 샘플링 비율을 적용해 평가해보았다. 기본 데이터셋에서 각 비율로 샘플링하여 부스팅 트리 모형을 학습시켰다. 서브 샘플링 비율을 {0.001, 0.01, 0.1, 0.5, 1}로 바꿔가며 적용했다.

데이터 크기 결과는 그림 10에 나와있다. 짐작했던 대로 데이터가 많을수록 성능은 향상된다. 그러나 예측 정확도 측면에서 데이터 크기에 따른 한계 이익은 감소한다. 데이터를 10 % 사용하면 전체 훈련 데이터셋 대비 정규화 엔트로피 성능은 1% 감소한다. 이 샘플링 비율에서 보정값 성능은 큰 손실 없다.

그림 10

그림 10: 데이터 크기에 대한 실험 결과. X축은 훈련 샘플 수에 해당한다. 왼쪽 y 주축에 눈금을 그렸고 표준화 엔트로피를 오른쪽 y 보조축에 표시했다.

6.2 음의 레이블에 대한 다운 샘플링

클래스 불균형은 많은 연구자가 탐구했고 학습 모형 성능에 중대한 영향을 미치는 것으로 나타났다. 클래스 불균형 문제를 해결하기 위해 음의 레이블에 대한 다운 샘플링을 적용해보았다. 학습시킨 모형 예측 정확도를 테스트하기 위해 음의 레이블에 대한 다운 샘플링 비율을 다양하게 직접 실험해보았다. 비율을 {0.1, 0.01, 0.001, 0.0001}로 바꿔가며 적용했다. 실험 결과는 그림 11과 같다.

그림 11

그림 11: 음의 레이블에 대한 다운 샘플링 실험 결과. X축은 여러 가지 음의 레이블에 대한 다운 샘플링 비율에 해당한다. 왼쪽 y 주축에 눈금을 그렸고 표준화 엔트로피는 오른쪽 y 보조축에 표시했다.

결과를 통해 음의 레이블에 대한 다운 샘플링 비율이 훈련 모형 성능에 중대한 영향을 미침을 알 수 있다. 음의 레이블에 대한 다운 샘플링 비율을 0.025로 설정했을 때 최고 성능을 얻었다.

6.3 모형 재보정

음의 레이블에 대한 다운 샘플링을 통해 훈련 속도를 높이고 모형 성능이 향상할 수 있다. 음의 레이블에 대한 다운 샘플링을 데이터셋에 적용하고 모형을 학습시키면 모형은 다운 샘플링된 공간 내에서 예측을 보정한다. 이 점을 염두에 둬야 한다. 예를 들어 샘플링 이전의 평균 CTR이 0.1%인데 음의 레이블에 대한 다운 샘플링을 0.01로 수행하면 경험적 CTR은 대략 10%가 된다. 실시간 트래픽 실험을 위해 모형을 재보정하고 \(q = {p \over p + (1 - p) / w}\)를 적용해 0.1% 예측으로 돌아가야 한다. 여기서 \(p\)는 다운 샘플링 공간 내에서의 예측이고 \(w\)는 음의 레이블에 대한 다운 샘플링 비율이다.

7. 논의

Facebook 광고 데이터를 실험하면서 몇 가지 실용적인 교훈을 얻을 수 있었다. 이 작업은 클릭 예측에 유용할 하이브리드 모형 아키텍처에 관한 영감을 주었다.

  • 데이터 신선도가 중요하다. 적어도 일별 재훈련시킬 가치가 있다. 본 논문은 다양한 온라인 학습 체계에 대해 상세히 논의했다. 또한 실시간 훈련 데이터를 생성할 수 있는 인프라를 제시했다.

  • 부스팅 결정 트리를 이용하여 실수 값 입력 변수를 변환하면 확률론적 선형 분류기 예측 정확도가 크게 향상할 수 있다. 이를 통해 부스팅 결정 트리와 희소 선형 분류기를 연결하는 하이브리드 모형 아키텍처에 관한 영감을 얻었다.

  • 최적 온라인 학습 방법: 좌표 별 학습률을 적용한 LR. BOPR과 성능이 비슷하며 연구했던 LR SGD 체계 중 가장 뛰어났다. (표 4, 그림 12)

대규모 기계 학습 응용 프로그램이 갖는 메모리 및 대기 시간을 적절히 유지하는 기술에 대해 설명했다.

  • 부스팅 결정 트리의 트리 개수와 정확도 간의 균형 관계를 제시했다. 계산 시간 및 메모리를 적절히 유지하기 위해서는 트리 개수를 적게 갖는 게 좋다.

  • 부스팅 결정 트리는 변수 중요도를 통해 변수 선택을 수행하는 편리한 방법을 제공한다. 이를 통해 사용하는 변수 개수를 과감히 줄이면서 예측 정확도 상의 큰 손실은 피할 수 있다.

  • 이력 변수 사용의 효과를 맥락 변수와 함께 분석했다. 관련 기록이 있는 광고 및 사용자의 경우 이력 변수는 맥락 변수보다 훨씬 뛰어난 예측 성능을 제공한다.

마지막으로 훈련 데이터를 서브 샘플링하는 방법 즉 양쪽 모두 균일하게, 보다 흥미롭게는 음의 레이블만 서브 샘플링하는 편향된 방식을 논의했다.

  1. J. Yi, Y. Chen, J. Li, S. Sett, and T. W. Yan. Predictive model performance: Offline and online evaluations. In KDD, pages 1294–1302, 2013. ↩

  2. T. Graepel, J. Quiñonero Candela, T. Borchert, and R. Herbrich. Web-scale bayesian click-through rate prediction for sponsored search advertising in Microsoft’s Bing search engine. In ICML, pages 13–20, 2010. ↩ ↩2

  3. H. B. McMahan, G. Holt, D. Sculley, M. Young, D. Ebner, J. Grady, L. Nie, T. Phillips, E. Davydov, D. Golovin, S. Chikkerur, D. Liu, M. Wattenberg, A. M. Hrafnkelsson, T. Boulos, and J. Kubica. Ad click prediction: a view from the trenches. In KDD, 2013. ↩ ↩2

  4. L. Golab and M. T. Özsu. Processing sliding window multi-joins in continuous queries over data streams. In VLDB, pages 500–511, 2003. ↩